
 如图,已知抛物线y=ax2+bx+c(a≠0)的图象过原点,并交x轴于A(-6,0),抛物线的顶点B的纵坐标为-$\sqrt{3}$.
如图,已知抛物线y=ax2+bx+c(a≠0)的图象过原点,并交x轴于A(-6,0),抛物线的顶点B的纵坐标为-$\sqrt{3}$.分析 (1)由题意可得x=0,y=0;x=-6,y=0,对称轴为x=-3,此时y=-$\sqrt{3}$,代入二次函数解析式,解方程组即可得到所求解析式,以及顶点的坐标;
(2)讨论当Q与B重合,显然成立;不重合,求得△AOB的形状,讨论Q在第一象限、第二象限,由任意角的三角函数的定义,即可求得Q的坐标,即可判断存在.
解答 解:(1)由题意可得x=0,y=0;x=-6,y=0,
对称轴为x=-3,此时y=-$\sqrt{3}$,
即有$\left\{\begin{array}{l}{c=0}\\{36a-6b+c=0}\\{9a-3b+c=-\sqrt{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{\sqrt{3}}{9}}\\{b=\frac{2\sqrt{3}}{3}}\\{c=0}\end{array}\right.$,
可得二次函数y=$\frac{\sqrt{3}}{9}$x2+$\frac{2\sqrt{3}}{3}$x,B(-3,-$\sqrt{3}$);
(2)当Q与B重合,△AQ0与△AOB相似;
当Q与B不重合,由△AOB为等腰三角形,
且tan∠AOB=$\frac{\sqrt{3}}{3}$,可得∠AOB=30°,∠ABO=120°,
若△AQ0与△AOB相似,
当Q在第二象限时,则∠QAO=120°,且△AQO为等腰三角形,
即有|AQ|=6,Q(-6-6cos60°,6sin60°),即为Q(-9,3$\sqrt{3}$);
当Q在第一象限时,则∠QOA=120°,且△AQO为等腰三角形,
即有|OQ|=6,Q(6cos60°,6sin60°),即为Q(3,3$\sqrt{3}$).
综上可得,在抛物线上存在点Q,且为(-3,-$\sqrt{3}$),或(-9,-3$\sqrt{3}$),(3,3$\sqrt{3}$),
使得△AQ0与△AOB相似.
点评 本题考查二次函数的解析式的求法,注意运用待定系数法,考查三角形的相似,注意运用三角函数的定义,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
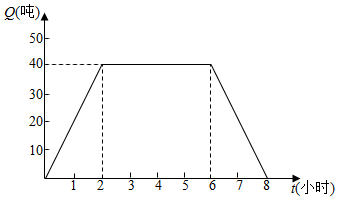 某游泳池先开进水管注水,使用完毕后开排水管排水,存水量Q(吨)与时间t(小时)之间的函数关系如图,则Q关于t的函数解析式为Q(t)=$\left\{\begin{array}{l}{20t,}&{0≤t≤2}\\{40,}&{2<t<5}\\{-\frac{40}{3}t+\frac{320}{3},}&{5<t≤8}\end{array}\right.$.
某游泳池先开进水管注水,使用完毕后开排水管排水,存水量Q(吨)与时间t(小时)之间的函数关系如图,则Q关于t的函数解析式为Q(t)=$\left\{\begin{array}{l}{20t,}&{0≤t≤2}\\{40,}&{2<t<5}\\{-\frac{40}{3}t+\frac{320}{3},}&{5<t≤8}\end{array}\right.$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 入学成绩(x/分) | 63 | 67 | 45 | 88 | 81 | 71 | 52 | 99 | 58 | 76 |
| 高一期末成绩(y/分) | 65 | 78 | 52 | 82 | 92 | 89 | 73 | 98 | 56 | 75 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com