
分析 当直线的斜率不存在时,求出直线方程检验是否满足条件;当直线的斜率存在时,由弦长公式求出圆心到直线的距离等于d,由此求得斜率,即得所求的直线方程.
解答 解:圆M:x2+(y+1)2=4的圆心为(0,-1),半径等于2.
当直线的斜率不存在时,直线方程为x=1,与圆的交点为(0,-1-$\sqrt{3}$),(0,-1+$\sqrt{3}$),弦长等于2$\sqrt{3}$,满足条件.
当直线的斜率存在时,设直线y-3=k(x-1),kx-y+3-k=0,设圆心到直线的距离等于d,
∵2$\sqrt{3}$=2$\sqrt{4-{d}^{2}}$,∴d=1,由点到直线的距离公式得$\frac{|1+3-k|}{\sqrt{{k}^{2}+1}}$=1,
∴k=$\frac{15}{8}$,直线为15x-8y+9=0.
综上,所求的直线方程为x=1,或15x-8y+9=0,
故答案为:x=1,或15x-8y+9=0.
点评 本题考查直线和圆的位置关系,点到直线的距离公式,弦长公式的应用,体现了分类讨论的数学思想.要注意考虑斜率不存在的情况.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≥3或-1≤x≤1} | B. | {x|x≥3或-1<x≤1} | C. | {x|x≤-3或-1≤x≤1} | D. | {x|x≤-3或-1<x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (-∞,0] | C. | (0,+∞) | D. | [0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
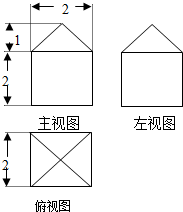
| A. | $(20+4\sqrt{3})c{m^2}$ | B. | $(20+4\sqrt{2})c{m^2}$ | C. | $(20+\sqrt{2})c{m^2}$ | D. | $(10+4\sqrt{2})c{m^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
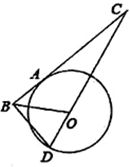 已知如图,A、D是⊙O上的点,A、B、C三点在一条直线上,直线CD经过圆心O,BD⊥BC,$\frac{BA}{AC}$=$\frac{DB}{DC}$.
已知如图,A、D是⊙O上的点,A、B、C三点在一条直线上,直线CD经过圆心O,BD⊥BC,$\frac{BA}{AC}$=$\frac{DB}{DC}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com