
| 第一批次 | 第二批次 | 第三批次 | |
| 女同学 | 196 | x | y |
| 男同学 | 204 | 156 | z |
分析 (1)利用等可能事件概率计算公式列出方程,由此能求出x.
(2)求出第三批次的人数为y+z=200,设第三批次中女教职工比男教职工多的事件为A,第三批次女教职工和男教职工数记为数对(y,z),由y+z=200,(y,z∈N,y≥96,z≥96),利用列举法求出基本事件总数和事件A包含的基本事件个数,由此能求出第三批次中女同学比男同学多的概率.
解答 解:(1)∵在全体教职工中随机抽取1名,抽到第二批次中女教职工的概率是0.16.
∴$\frac{x}{900}=0.16$,解得x=144.
(2)第三批次的人数为y+z=900-(196+204+144+156)=200,
设第三批次中女教职工比男教职工多的事件为A,
第三批次女教职工和男教职工数记为数对(y,z),
由y+z=200,(y,z∈N,y≥96,z≥96),
则基本事件总数有:(96,104),(97,103),(98,102),(99,101),
(100,100),(101,99),(102,98),(103,97),(104,96),共9个,
而事件A包含的基本事件有:(101,99),(102,98),(103,97),(104,96)共4个,
∴第三批次中女同学比男同学多的概率P(A)=$\frac{4}{9}$.
点评 本题考查实数值的求法,考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式、列举法的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | .y=sin2x | B. | .y=-sin2x | C. | .y=cos2x | D. | y=-2cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (-∞,0) | C. | (-∞,0)∪(2,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
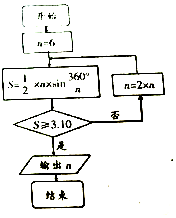 如图是利用我国古代数学家刘徽的割圆术设计的程序框图,则输出的n值为( )
如图是利用我国古代数学家刘徽的割圆术设计的程序框图,则输出的n值为( )| A. | 12 | B. | 24 | C. | 48 | D. | 96 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{3}{5}$ | D. | -$\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com