
分析 (1)由椭圆的离心率e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\sqrt{1-\frac{1}{{a}^{2}}}$=$\frac{\sqrt{3}}{2}$,求得a,求得椭圆方程,当y1=0时,直线x1=±2,求得PA的方程是x=±2,当y1≠0时,求导,求得PA的切线斜率,根据直线的点斜式方程及x12+4y12=4,即可求得$\frac{{x}_{1}x}{4}$+y1y=1;
(2)由(1)可知:切线PB 的方程为$\frac{{x}_{2}x}{4}+{y}_{2}y=1$,代入求得直线AB方程,代入椭圆方程,求得弦长丨AB丨,根据点到直线的距离公式d,由S△OAB=$\frac{1}{2}$•丨AB丨•d=$\frac{4\sqrt{3{n}^{2}+12}}{3{n}^{2}+16}$,由均值不等式,即可求得△OAB面积的最大值.
解答 解:(1)证明:离心率e=$\frac{c}{a}$=$\sqrt{\frac{{c}^{2}}{{a}^{2}}}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\sqrt{1-\frac{1}{{a}^{2}}}$=$\frac{\sqrt{3}}{2}$,
∴a=2,
椭圆方程为:$\frac{{x}^{2}}{4}+{y}^{2}=1$,
当y1=0时,直线x1=±2,
∴x2=4,代入椭圆方程得到y=0,
∴切线PA的方程是x=±2;
当y1≠0时,对椭圆方程两边求导得:$\frac{x}{2}+2yy′=0$,
则过切点A的斜率为k=y′=-$\frac{{x}_{1}}{4{y}_{1}}$,
切线方程为:y-y1=-$\frac{{x}_{1}}{4{y}_{1}}$(x-x1),
∵又x12+4y12=4,
∴$\frac{{x}_{1}x}{4}$+y1y=1;
(2)根据(1)可得切线 PA的方程为 $\frac{{x}_{1}x}{4}$+y1y=1,
切线PB 的方程为$\frac{{x}_{2}x}{4}+{y}_{2}y=1$,
∴$\left\{\begin{array}{l}{\frac{{x}_{1}m}{4}+{y}_{1}n=1}\\{\frac{{x}_{2}m}{4}+{y}_{2}n=1}\end{array}\right.$,
∴直线 AB方程为 $\frac{mx}{4}+ny=1$,
∴$\left\{\begin{array}{l}{\frac{mx}{4}+ny=1}\\{{x}^{2}+4{y}^{2}-4=0}\end{array}\right.$,消y 得到(1+$\frac{{m}^{2}}{4{n}^{2}}$)2-$\frac{2m}{{n}^{2}}$x+$\frac{4}{{n}^{2}}$-4=0,
∴丨AB丨=$\sqrt{1+{k}^{2}}$•$\frac{\sqrt{△}}{丨a丨}$=$\sqrt{1+(-\frac{m}{4n})^{2}}$•$\frac{\sqrt{-\frac{16}{{n}^{2}}+\frac{4{m}^{2}}{{n}^{2}}+16}}{丨1+\frac{{m}^{2}}{4{n}^{2}}丨}$,
又∵原点 O到直线AB 的距离d=$\frac{1}{\sqrt{\frac{{m}^{2}}{{4}^{2}}+{n}^{2}}}$,
∴S△OAB=$\frac{1}{2}$•丨AB丨•d=$\sqrt{1+(-\frac{m}{4n})^{2}}$•$\frac{\sqrt{-\frac{16}{{n}^{2}}+\frac{4{m}^{2}}{{n}^{2}}+16}}{丨1+\frac{{m}^{2}}{4{n}^{2}}丨}$•$\frac{1}{\sqrt{\frac{{m}^{2}}{{4}^{2}}+{n}^{2}}}$,
=$\frac{4\sqrt{4{n}^{2}+{m}^{2}-4}}{4{n}^{2}+{m}^{2}}$,
又∵P(m,n) 为圆x2+y2=16上任意一点,
∴m2+n2=16,
∴S△OAB=$\frac{4\sqrt{3{n}^{2}+12}}{3{n}^{2}+16}$,
令t=$\sqrt{3{n}^{2}+12}$≥2$\sqrt{3}$,则S△OAB=$\frac{4t}{{t}^{2}+4}$=$\frac{4}{t+\frac{4}{t}}$ 在[2$\sqrt{3}$,+∞) 上单调递减,
∴S△OAB≤$\frac{\sqrt{3}}{2}$.
点评 本题考查椭圆的标准方程及简单性质,直线与椭圆的位置关系,考查弦长公式,点到直线的位置关系及三角形的面积公式的综合运用,难度系数较大,在高考中属于压轴题,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | (-2,+∞) | B. | (0,+∞) | C. | (-∞,0) | D. | (-∞,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
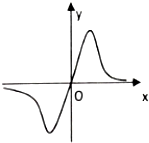 函数f(x)=$\frac{ax+b}{x^2+c}$的图象如图所示,则下列结论成立的是( )
函数f(x)=$\frac{ax+b}{x^2+c}$的图象如图所示,则下列结论成立的是( )| A. | a>0,c>0 | B. | a>0,c<0 | C. | a<0,c>0 | D. | a<0,c<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$-1 | B. | $\sqrt{2}$ | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
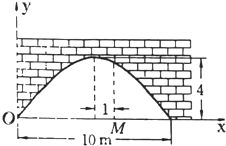 有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为 4m,跨度为 10m,把它的图形放在如图所示直角坐标系中.
有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为 4m,跨度为 10m,把它的图形放在如图所示直角坐标系中.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com