
(本小题满分14分)
已知向量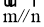 ,其中
,其中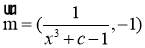 ,
,
 ,把其中
,把其中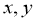 所满足的关系式记为
所满足的关系式记为 ,且函数
,且函数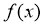 为奇函数.
为奇函数.
(1)求函数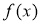 的表达式;
的表达式;
(2)已知数列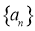 的各项都是正数,
的各项都是正数,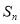 为数列
为数列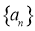 的前
的前 项和,且对于任意
项和,且对于任意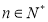 ,都有“数列
,都有“数列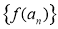 的前
的前 项和”等于
项和”等于 ,求数列
,求数列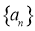 的首项
的首项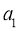 和通项公式
和通项公式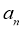 ;
;
(3)若数列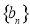 满足
满足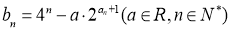 ,求数列
,求数列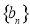 的最小值.
的最小值.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) ;(Ⅲ)详见解析.
;(Ⅲ)详见解析.
【解析】
试题分析:(Ⅰ)根据向量平行得出函数 ,再利用函数
,再利用函数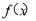 为奇函数,可求c=1,从而可得函数
为奇函数,可求c=1,从而可得函数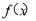 的表达式;
的表达式;
(Ⅱ)根据条件对于任意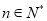 ,都有
,都有 的前n项和等于
的前n项和等于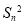 ,写出两等式,两式相减可得
,写出两等式,两式相减可得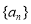 为公差为1的等差数列,从而可求数列
为公差为1的等差数列,从而可求数列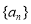 的通项公式;
的通项公式;
(Ⅲ)根据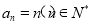 ,可得
,可得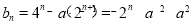 ,由于
,由于 ,故需对
,故需对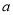 进行分类讨论.
进行分类讨论.
试题解析:(Ⅰ)∵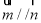 ,∴
,∴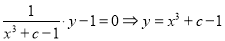
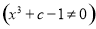 ,
,
因为函数f(x)为奇函数.所以c=1,故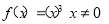
(Ⅱ)由题意可知, …..①
…..①
n≥2时,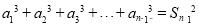 …②
…②
由①﹣②可得: ,
,
∵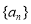 为正数数列,∴
为正数数列,∴ …③,∴
…③,∴ …④
…④
由④﹣③可得: ,
,
且由①可得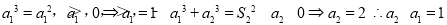
∴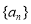 为公差为1的等差数列,∴
为公差为1的等差数列,∴ ;
;
(Ⅲ)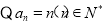 ,
,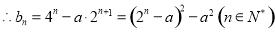
令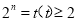 ,∴
,∴
(1)当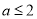 时,数列
时,数列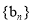 的最小值为当n=1时,
的最小值为当n=1时, .
.
(2)当a>2时
①若 时,数列
时,数列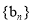 的最小值为当n=k+1时,
的最小值为当n=k+1时, .
.
②若 时,数列
时,数列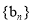 的最小值为当n=k或n=k+1时,
的最小值为当n=k或n=k+1时, .
.
③若 
 时,数列
时,数列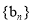 的最小值为当n=k时,
的最小值为当n=k时,
④若 时,数列{bn}的最小值为,当n=k+1时,
时,数列{bn}的最小值为,当n=k+1时, .
.
考点:向量共线定理;数列通项公式;函数的最值问题;数列与向量的综合;分类讨论思想.


科目:高中数学 来源:2014-2015学年福建省四地六校高三上学期第三次月考理科数学试卷(解析版) 题型:选择题
如图,正方体ABCD—A1B1C1D1中,O为底面ABCD的中心,
M为棱BB1的中点,则下列结论中错误的是( )
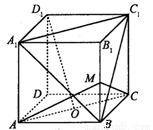
A.D1O∥平面A1BC1
B.D1O⊥平面AMC
C.异面直线BC1与AC所成的角等于60°
D.二面角M-AC-B等于45°
查看答案和解析>>
科目:高中数学 来源:2014-2015学年黑龙江省绥化市三校高二上学期期中联考数学试卷(解析版) 题型:选择题
一个圆的圆心为椭圆的右焦点F,且该圆过椭圆的中心交椭圆于点P, 直线PF (F
(F 为椭圆的左焦点)是该圆的切线,则椭圆的离心率为( )
为椭圆的左焦点)是该圆的切线,则椭圆的离心率为( )
A. B.
B. C.
C. D.
D.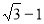
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省揭阳市高一上学期期中考试数学试卷(解析版) 题型:选择题
函数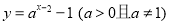 的图象必经过点( ).
的图象必经过点( ).
A.(0,1) B.(1,1) C.(2, 0) D.(2,2)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省揭阳市高二上学期期中考试理科数学试卷(解析版) 题型:解答题
(本题满分12分)已知等差数列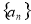 的前
的前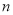 项和为
项和为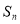 ,其中
,其中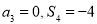 .
.
(1)求数列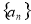 的通项公式;
的通项公式;
(2)当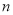 为何值时,
为何值时, 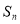 取得最小值.
取得最小值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省揭阳市高二上学期期中考试理科数学试卷(解析版) 题型:选择题
若函数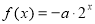 与
与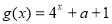 的图象有交点,则
的图象有交点,则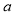 的取值范围是( )
的取值范围是( )
A.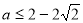 或
或 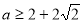
B.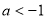
C.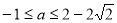
D.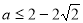
查看答案和解析>>
科目:高中数学 来源:2015届江苏教育学院附属高中高三上学期期中文科数学试卷(解析版) 题型:解答题
(本题满分14分)设函数f(x)=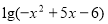 的定义域为A,函数g(x)=
的定义域为A,函数g(x)=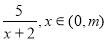 的值域为B.
的值域为B.
(Ⅰ)当m=2时,求A∩B;
(Ⅱ)若“x∈A”是“x∈B”的必要不充分条件,求实数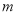 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com