
分析 (Ⅰ)由a2=$\frac{2{a}^{2}}{4a-1}$>$\frac{1}{2}$可解得a>$\frac{1}{4}$且a≠$\frac{1}{2}$,从而利用归纳法求解即可;
(Ⅱ)可判断出$\frac{1}{2}$<an<1,n≥2;从而分类讨论证明即可.
解答 解:(Ⅰ)∵a1=a,∴a2=$\frac{2{a}^{2}}{4a-1}$>$\frac{1}{2}$,
解得,a>$\frac{1}{4}$且a≠$\frac{1}{2}$,
∵当a>$\frac{1}{2}$时,$\frac{2{a}^{2}}{4a-1}$>$\frac{1}{2}$,
∴对任意的n∈N*,都有an+1>$\frac{1}{2}$,
故实数a的取值范围为($\frac{1}{4}$,$\frac{1}{2}$)∪($\frac{1}{2}$,+∞);
(Ⅱ)证明:∵a1=a=1,
∴a2=$\frac{2}{4-1}$=$\frac{2}{3}$,
由(Ⅰ)知,an>$\frac{1}{2}$恒成立,
an+1-an=$\frac{2{a}_{n}^{2}}{4{a}_{n}-1}$-an=$\frac{{a}_{n}(1-2{a}_{n})}{4{a}_{n}-1}$<0,
∴$\frac{1}{2}$<an<1,n≥2;
当n=1时,S1<$\frac{1}{4}$+1,
当n=2时,S2=1+$\frac{2}{3}$<2;
当n≥3时,Sn<n,而$\frac{{n}^{2}}{4}$+1>2•$\frac{n}{2}$•1=n,
故Sn<$\frac{{n}^{2}}{4}$+1,
综上所述,Sn<$\frac{{n}^{2}}{4}$+1恒成立.
点评 本题考查了不等式的解法,数列的性质的判断,同时考查了归纳法与分类讨论的思想方法应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
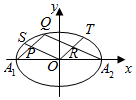 如图,A1,A2为椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS围成一个平行四边形OPQR,则|OS|2+|OT|2=( )
如图,A1,A2为椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS围成一个平行四边形OPQR,则|OS|2+|OT|2=( )| A. | 5 | B. | 3+$\sqrt{5}$ | C. | 9 | D. | 14 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com