
分析 (1)根据等差数列定义和求和公式,即可求出,
(2)利用递推公式即可求出数列{bn}的通项公式,再根据错位相减法求出数列{bn}的前n项和Tn.
解答 解:(1)由$\left\{\begin{array}{l}{S_4}=4{S_2}\\{a_{2n}}=2{a_n}+1\end{array}\right.$得$\left\{\begin{array}{l}4{a_1}+\frac{1}{2}×4×3d=4(2{a_1}+d)\\{a_1}+(2n-1)d=2{a_1}+2(n-1)d+1\end{array}\right.$
即$\left\{\begin{array}{l}2{a_1}=d\\{a_1}-d+1=0\end{array}\right.$,
解得$\left\{\begin{array}{l}{a_1}=1\\ d=2\end{array}\right.$,
故通项an=2n-1
(2)由已知$\frac{b_1}{a_1}+\frac{b_2}{a_2}+\frac{b_3}{a_3}+…+\frac{b_n}{a_n}=1-\frac{1}{2^n}\;\;\;(n∈{N^*})$①
n=1时,$\frac{b_1}{a_1}=\frac{1}{2}$,
n≥2时,$\frac{b_1}{a_1}+\frac{b_2}{a_2}+\frac{b_3}{a_3}+…+\frac{{{b_{n-1}}}}{{{a_{n-1}}}}=1-\frac{1}{{{2^{n-1}}}}\;\;\;(n∈{N^*})$②
①-②得:$\frac{b_n}{a_n}=1-\frac{1}{2^n}-(1-\frac{1}{{{2^{n-1}}}})=\frac{1}{2^n}$,
对于n=1也成立
故$\frac{b_n}{a_n}=\frac{1}{2^n}\;\;\;(n∈{N^*})$
所以${b_n}=(2n-1)\frac{1}{2^n}\;\;\;(n∈{N^*})$,
${T_n}=\frac{1}{2}+\frac{3}{2^2}+\frac{5}{2^3}+…+\frac{2n-1}{2^n}$③,
$\frac{1}{2}{T_n}=\frac{1}{2^2}+\frac{3}{2^3}+\frac{5}{2^4}+…+\frac{2n-1}{{{2^{n+1}}}}$④,
③-④得:$\frac{1}{2}{T_n}=\frac{1}{2}+2(\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+…+\frac{1}{2^n})-\frac{2n-1}{{{2^{n+1}}}}$=$\frac{1}{2}+2×\frac{{\frac{1}{4}-\frac{1}{{{2^{n+1}}}}}}{{1-\frac{1}{2}}}-\frac{2n-1}{{{2^{n+1}}}}$=$\frac{3}{2}-\frac{4}{{{2^{n+1}}}}-\frac{2n-1}{{{2^{n+1}}}}$=$\frac{3}{2}-\frac{2n+3}{{{2^{n+1}}}}$
所以${T_n}=3-\frac{2n+3}{2^n}$
点评 本题考查等差数列的定义,等差等比数列求和等基础知识,考查计算能力、推理论证能力、综合发现问题解决问题的能力以及分类讨论思想


科目:高中数学 来源: 题型:填空题
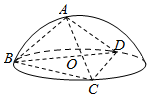 如图,半球O内有一内接正三棱锥A-BCD(底面△BCD为等边三角形,顶点A在底面的射影为ABCD的中心),且△BCD内接于圆O,当半球O的体积为2$\sqrt{3}$π时,三棱锥A-BCD的所有棱长之和为9+3$\sqrt{6}$.
如图,半球O内有一内接正三棱锥A-BCD(底面△BCD为等边三角形,顶点A在底面的射影为ABCD的中心),且△BCD内接于圆O,当半球O的体积为2$\sqrt{3}$π时,三棱锥A-BCD的所有棱长之和为9+3$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,-$\frac{1}{2}$] | B. | (-∞,1) | C. | [$\frac{1}{2}$,1) | D. | (-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{1}{8}$ | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com