
已知曲线 的极坐标方程是
的极坐标方程是 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴正方向建立平面直角坐标系,直线l的参数方程是
轴正方向建立平面直角坐标系,直线l的参数方程是 (
( 为参数).
为参数).
(1)求曲线 的直角坐标方程;
的直角坐标方程;
(2)设直线l与曲线 交于
交于 、
、 两点,点
两点,点 的直角坐标为(2,1),若
的直角坐标为(2,1),若 ,求直线l的普通方程.
,求直线l的普通方程.
(1) ;(2)
;(2) 或
或
【解析】
试题分析:(1)由曲线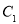 的极坐标方程是
的极坐标方程是 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴正方向建立平面直角坐标系,在极坐标方程两边同乘以
轴正方向建立平面直角坐标系,在极坐标方程两边同乘以 ,根据极坐标与普通方程相互转化的等式关系可得求曲线
,根据极坐标与普通方程相互转化的等式关系可得求曲线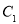 的直角坐标方程.
的直角坐标方程.
(2)直线l与曲线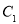 交于
交于 、
、 两点,点
两点,点 的直角坐标为(2,1),若
的直角坐标为(2,1),若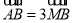 ,所以
,所以 .即直线方程与圆的方程联立即可得到一个关于t的方程,再由
.即直线方程与圆的方程联立即可得到一个关于t的方程,再由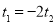 以及韦达定理即可得到结论.
以及韦达定理即可得到结论.
(1)由 ,得
,得 ,
,
 ,
,
 曲线
曲线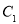 的直角坐标方程是
的直角坐标方程是 ,即
,即 . 3分
. 3分
(2)设 ,
, ,
,
由已知 ,得
,得 ① 4分
① 4分
联立直线的参数方程与曲线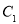 的直角坐标方程得:
的直角坐标方程得: ,
,
整理得: ,
, ,与①联立得:
,与①联立得:
 ,
,
 直线的参数方程为
直线的参数方程为 (
( 为参数)或
为参数)或 (
( 为参数)
为参数)
消去参数的普通方程为 或
或 7分
7分
考点:1.极坐标方程.2.参数方程.3.直线与圆的位置关系.


科目:高中数学 来源:2014-2015学年重庆市高二10月定时练习文科数学试卷(解析版) 题型:解答题
(1)已知两条直线 ,
, 平行,求实数
平行,求实数 的值
的值
(2)过原点且倾斜角为45°的直线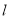 与圆C:
与圆C: 相交于点
相交于点 ,求弦长
,求弦长
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高三高考压轴理科数学试卷(解析版) 题型:选择题
为调查某校学生喜欢数学课的人数比例,采用如下调查方法:
(1)在该校中随机抽取100名学生,并编号为1,2,3, ,100;
(2)在箱内放置两个白球和三个红球,让抽取的100名学生分别从箱中随机摸出一球,记住其颜色并放回;
(3)请下列两类学生举手:(ⅰ)摸到白球且号数为偶数的学生;(ⅱ)摸到红球且不喜欢数学课的学生.
如果总共有26名学生举手,那么用概率与统计的知识估计,该校学生中喜欢数学课的人数比例大约是( )
A.88% B.90% C.92% D.94%
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高三高考压轴文科数学试卷(解析版) 题型:选择题
已知双曲线 的一条渐近线与函数
的一条渐近线与函数 的图象相切,则双曲线
的图象相切,则双曲线 的离心率等于( )
的离心率等于( )
A. B.
B.
 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高三高考压轴文科数学试卷(解析版) 题型:选择题
已知命题 :?
:? ,
, ,则下列说法正确的是( )
,则下列说法正确的是( )
A. :?
:? ,
, ,且
,且 为假命题
为假命题
B. :?
:? ,
, ,且
,且 为真命题
为真命题
C. :?
:? ,
, ,且
,且 为假命题
为假命题
D. :?
:? ,
, ,且
,且 为真命题
为真命题
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省福州市高三5月综合练习理科数学试卷(解析版) 题型:解答题
在 中,
中, 的对边分别是
的对边分别是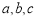 ,已知
,已知 ,平面向量
,平面向量 ,
, ,且
,且 .
.
(1)求△ABC外接圆的面积;
(2)已知O为△ABC的外心,由O向边BC、CA、AB引垂线,垂足分别为D、E、F,求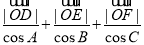 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省福州市高三5月综合练习理科数学试卷(解析版) 题型:选择题
在密码理论中,“一次一密”的密码体系是理论上安全性最高的.某部队执行特殊任务使用四个不同的口令 ,每次只能使用其中的一种,且每次都是从上次未使用的三个口令中等可能地随机选用一种.设第1次使用
,每次只能使用其中的一种,且每次都是从上次未使用的三个口令中等可能地随机选用一种.设第1次使用 口令,那么第5次也使用
口令,那么第5次也使用 口令的概率是( )
口令的概率是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高考考前模拟文科数学试卷(解析版) 题型:解答题
某同学用“五点法”画函数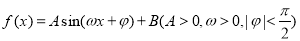 在某一
在某一
个周期内的图象时,列表并填入的部分数据如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请求出上表中的 ,并直接写出函数
,并直接写出函数 的解析式;
的解析式;
(2)将 的图象沿
的图象沿 轴向右平移
轴向右平移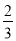 个单位得到函数
个单位得到函数 ,若函数
,若函数 在
在 (其中
(其中 )上的值域为
)上的值域为 ,且此时其图象的最高点和最低点分别为
,且此时其图象的最高点和最低点分别为 ,求
,求 与
与 夹角
夹角 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com