考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由椭圆的离心率e=
,得椭圆方程为
+=1,把点(1,
)代入,能求出椭圆的方程.
(2)设直线l为y=k(x-1),代入椭圆方程
+=1,得(3+4k
2)x
2-8k
2x+4k
2-12=0,由此利用根的判别式、韦达定理,结合已知条件能求出直线MN的方程.
解答:
解:(1)∵椭圆C:
+
=1(a>b>0)过点(1,
),
F
1、F
2分别为椭圆C的左、右两个焦点,且离心率e=
,
∴
=,∴a=2c,∴b
2=a
2-c
2=3c
2,
∴椭圆方程为
+=1.…(2分)
把点(1,
)代入椭圆,得
+=1,解得c
2=1.
∴椭圆的方程为
+=1.…(4分)
(2)若直线l斜率不存在,
k1 +k2=0不合题意,
∴直线l的斜率存在.…(5分)
设直线l为y=k(x-1),代入椭圆方程
+=1,
得(3+4k
2)x
2-8k
2x+4k
2-12=0.…(7分)
依题意△=9k
2+9>0.
设M(x
1,y
1),N(x
2,y
2),则
x1+x2=,
x1x2=.…(8分)
∵k
1+k
2=-3,
∴k
1+k
2=
+=k(
+)
=k(2-
)
=k(2-
)=-3.…(10分)
整理,得k
2-2k-3=0,解得k=3或k=-1.
∴所求直线MN的方程为3x-y-3=0或x+y-1=0.…(12分)
点评:本题考查椭圆方程的求法,考查直线方程的求法,解题时要认真审题,注意韦达定理的灵活运用.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案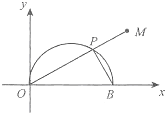 在直角坐标xoy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2cosθ,如图,曲线C与x轴交于O,B两点,P是曲线C在x轴上方图象上任意一点,连结OP并延长至M,使PM=PB,当P变化时,求动点M的轨迹的长度.
在直角坐标xoy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2cosθ,如图,曲线C与x轴交于O,B两点,P是曲线C在x轴上方图象上任意一点,连结OP并延长至M,使PM=PB,当P变化时,求动点M的轨迹的长度.