Question

1．若满足x，y约束条件$\left\{\begin{array}{l}{x-y+1≤0}\\{x-2y≤0}\\{x+2y-2≤0}\end{array}\right.$，则z=x+y的最大值为（　　）

• A． $\frac{3}{2}$
• B． 1
• C． -1
• D． -3

Answer 1

分析 由约束条件作出可行域，数形结合得到最优解，求出最优解的坐标，代入目标函数得答案．

解答 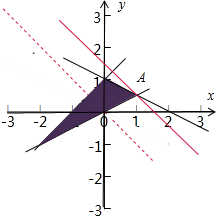解：由约束条件$\left\{\begin{array}{l}{x-y+1≤0}\\{x-2y≤0}\\{x+2y-2≤0}\end{array}\right.$作出可行域如图，

化目标函数z=x+y为y=-x+z，
由图可知，当直线y=-x+z过A时，目标函数有最大值，
由：$\left\{\begin{array}{l}{x-2y=0}\\{x+2y-2=0}\end{array}\right.$，可得A（1，$\frac{1}{2}$），z的最大值为z=1+$\frac{1}{2}$=$\frac{3}{2}$．
故选：A．

点评 本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．