练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．已知${（1-2x）^6}={a_0}+{a_1}x+{a_2}{x^2}+{a_3}{x^3}+{a_4}{x^4}+{a_5}{x^5}+{a_6}{x^6}$，则|a0|+|a1|+|a2|+|a3|+|a4|+|a5|+|a6|的值为（　　）
    A．729B．243C．64D．1

    分析 利用赋值法，x=-1，代入求解即可．

    解答 解：${（1-2x）^6}={a_0}+{a_1}x+{a_2}{x^2}+{a_3}{x^3}+{a_4}{x^4}+{a_5}{x^5}+{a_6}{x^6}$，
    x=-1时，则|a0|+|a1|+|a2|+|a3|+|a4|+|a5|+|a6|=36=729．
    故选：A．

    点评 本题考查二项式定理的应用，赋值法的应用，考查计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    1．给出下列三个结论：
    ①设回归直线方程为$\widehat{y}$=2-2.5x，当变量x增加1个单位时，y平均增加2个单位；
    ②若命题p：?x0∈[1，+∞），$x_0^2-{x_0}-1＜0$，则￢p：?x∈（-∞，1），x2-x-1≥0；
    ③已知直线l1：ax+3y-1=0，l2：x+by+1=0，则l1⊥l2的充要条件是$\frac{a}{b}=-3$；
    其中正确结论的个数为（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．过椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的一个焦点作垂直于长轴的弦，则此弦长为3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．化简：$\frac{{2cos（{\frac{π}{2}-α}）+sin（{π-2α}）}}{{2co{s^2}\frac{α}{2}}}$=2sinα．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知正方形ABCD的边长是a，依次连接正方形ABCD的各边中点得到一个新的正方形，再依次连接新正方形的各边中点又得到一个新的正方形，按此规律，依次得到一系列的正方形，如图所示，现有一只小虫从A点出发，沿正方形的边逆时针方向爬行，每遇到新正方形的顶点时，沿这个新正方形的边逆时针方向爬行，如此下去，爬行了10条线段，则这10条线段的长度的和是（　　）
    A．$\frac{31}{128}（2+\sqrt{2}）a$B．$\frac{31}{64}（2+\sqrt{2}）a$C．$（1+\frac{{\sqrt{2}}}{32}）a$D．$（1-\frac{{\sqrt{2}}}{32}）a$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数y=3sin3x．
    （1）求f（x）的最小正周期；
    （2）求f（x）的单调递增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．设集合A={2}，B={x|ax-1=0，a∈R}，若A∩B=B，则a=0或$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

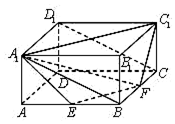    7．如图，在长方体ABCD-A1B1C1D1中，AA1=1，AB=AD=2，E，F分别是棱AB，BC的中点，证明A1，C1，F，E四点共面，并求点B到平面A1EF的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．在△ABC中，内角A、B、C所对的边分别是a、b、c，不等式${x^2}cosC+2xsinC+\frac{3}{2}≥0$对一切实数x恒成立．
    （1）求cosC的取值范围；
    （2）当∠C取最大值，且△ABC的周长为9时，求△ABC面积的最大值，并指出面积取最大值时△ABC的形状．

    查看答案和解析>>

    同步练习册答案