
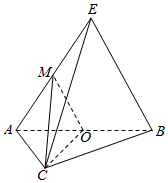
 如图,在三棱锥E-ABC中,平面EAB⊥平面ABC,三角形EAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB、EA中点.
如图,在三棱锥E-ABC中,平面EAB⊥平面ABC,三角形EAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB、EA中点.分析 (1)由中位线定理可得OM∥BE,故而EB∥平面MOC;
(2)由等腰三角形三线合一可得OC⊥AB,由平面EAB⊥平面ABC可得OC⊥平面EAB,故而平面MOC⊥平面EAB;
(3)连结OE,则OE为棱锥的高,利用等边三角形的性质求出OE,代入体积计算.
解答 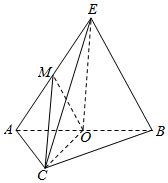 证明:(1)证明:∵O,M分别为AB,EA的中点,∴OM∥BE,
证明:(1)证明:∵O,M分别为AB,EA的中点,∴OM∥BE,
又∵EB?平面MOC,OM?平面MOC,
∴EB∥平面MOC.
(2)∵AC=BC,O 为AB中点,∴OC⊥AB,
又∵平面EAB⊥平面ABC,平面EAB∩平面ABC=AB,
∴OC⊥平面EAB,又∵OC?平面MOC,
∴平面MOC⊥平面 EAB.
(3)连结OE,则OE⊥AB,
又∵平面EAB⊥平面ABC,平面EAB∩平面ABC=AB,OE?平面EAB,
∴OE⊥平面ABC.
∵AC⊥BC,AC=BC=$\sqrt{2}$,∴AB=2,
∵三角形EAB为等边三角形,∴OE=$\sqrt{3}$.
∴三棱锥E-ABC的体积V=$\frac{1}{3}{S}_{△ABC}$•EO=$\frac{1}{3}×\frac{1}{2}×\sqrt{2}×\sqrt{2}×\sqrt{3}$=$\frac{\sqrt{3}}{3}$.
点评 本题考查了线面平行,线面垂直的判定,面面垂直的性质,棱锥的体积计算,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | $\frac{5}{2}\sqrt{2}$ | D. | $\frac{3}{2}\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
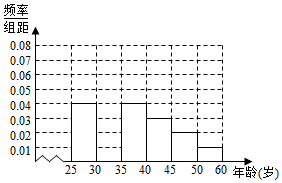 某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为:非低碳族“,得到如下统计表和各年龄段人数频率分布直方图:
某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为:非低碳族“,得到如下统计表和各年龄段人数频率分布直方图:| 组数 | 分组 | 低碳族 的人数 | 占本组 的频率 |
| 1 | [25,30) | 120 | 0.6 |
| 2 | [30,35) | 195 | P |
| 3 | [35,40) | 100 | 0.5 |
| 4 | [40,45) | a | 0.4 |
| 5 | [45,50) | 30 | 0.3 |
| 6 | [50,55) | 15 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有2个 | B. | 有4个 | C. | 不一定存在 | D. | 一定不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
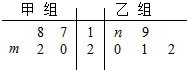 某车间将10名工人评价分成甲、乙两组加工某种零件,在单位时间内每个工人加工的合格零件数如茎叶图所示.已知两组工人在单位时间内加工的合格零件平均数都为20,则有( )
某车间将10名工人评价分成甲、乙两组加工某种零件,在单位时间内每个工人加工的合格零件数如茎叶图所示.已知两组工人在单位时间内加工的合格零件平均数都为20,则有( )| A. | m=3,n=8 | B. | m=4,n=7 | C. | m=5,n=6 | D. | m=6,n=5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 线段CD的中点 | B. | 线段CD靠近C的四等分点 | ||
| C. | 重心 | D. | 线段CD靠近C的三等分点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com