
| A. | 2 | B. | 4 | C. | $\frac{5}{2}\sqrt{2}$ | D. | $\frac{3}{2}\sqrt{2}$ |
分析 求得椭圆的a,b,c,由题意可得P的坐标,再由椭圆的定义计算即可得到所求值.
解答 解:椭圆${x^2}+\frac{y^2}{2}=1$的a=$\sqrt{2}$,b=1,c=1,
由PF1⊥F1F2,可得yP=-1,xP=±$\sqrt{1-\frac{1}{2}}$=±$\frac{\sqrt{2}}{2}$,
即有|PF1|=$\frac{\sqrt{2}}{2}$,
由题意的定义可得,|PF2|=2a-|PF1|=2$\sqrt{2}$-$\frac{\sqrt{2}}{2}$=$\frac{3\sqrt{2}}{2}$.
故选:D.
点评 本题考查椭圆的方程的运用,以及椭圆的定义,考查运算能力,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[-2,\sqrt{3}]$ | B. | $[-\frac{{\sqrt{3}}}{2},1]$ | C. | $[-\sqrt{3},\sqrt{3}]$ | D. | $[-\frac{{\sqrt{3}}}{2},\sqrt{3}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y={x^{\frac{2016}{2015}}}$ | B. | $y={x^{\frac{2013}{2015}}}$ | C. | $y={x^{-\frac{2014}{2015}}}$ | D. | $y={x^{-\frac{2015}{2016}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
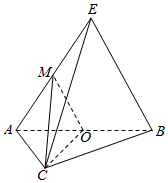 如图,在三棱锥E-ABC中,平面EAB⊥平面ABC,三角形EAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB、EA中点.
如图,在三棱锥E-ABC中,平面EAB⊥平面ABC,三角形EAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB、EA中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com