
���� ��1��������������ƽ�е������ϵ�õ�Sn=��an-1��bn����һ����nȡֵ���õ�����{an}�ǵȲ����У�
��2������${b_n}=\frac{n}{2}$����2Sn=nan-n�ۣ���2Sn+1=�� n+1��an+1-��n+1���ܣ���ʽ������ɵõ�����{an}�ĵ��ƹ�ʽ����һ����n ȡֵ���õ�����{an}������Ϊ-1������Ϊ1�ĵȲ����У�
���ɢٵõ�����{cn}ͨ�ʽ������m��l�ķ�Χ���ۿ��ܵ�ȡֵ��
��� �⣺��1����Ϊ$\overrightarrow{x}$=��1��bn����$\overrightarrow{y}$=��an-1��Sn����$\overrightarrow{x}$��$\overrightarrow{y}$��
��Sn=��an-1��bn����bn=2����Sn=2an-2 �٣�
��n=1ʱ��S1=2a1-2����a1=2������1�֣�
��Sn+1=2an+1-2 �ڣ�
��-�ٵ�Sn+1-Sn=2an+1-2an��
��an+1=2an����a1=2��
����{an}������Ϊ2������Ϊ2�ĵȱ����У�����3�֣�
����an=2n������4�֣�
��2����֤������Ϊ${b_n}=\frac{n}{2}$����2Sn=nan-n�ۣ�
��n=1ʱ��2S1=a1-1����a1=-1��
��2Sn+1=�� n+1��an+1-��n+1���ܣ�
��-�۵�
2Sn+1-2Sn=��n+1��an+1-nan-1������6�֣�
����n-1��an+1-nan-1=0 �ݣ�
��nan+2-��n+1��an+1-1=0��
��-�ݵã�nan+2-2nan+1+nan=0��
��an+2+an=2an+1����������{an}�ǵȲ����У�����8�֣�
����a1=-1��a2=0��
��������{an}������Ϊ-1������Ϊ1�ĵȲ����У�
an=-1+��n-1����1=n-2������${c_n}=\frac{n+1}{n}$������10�֣�
�������l��m��l��2��m��2����ʹ��cl��c2��cm�ɵȱ����У���$c_2^2={c_l}{c_m}$��
�ɵ�$\frac{9}{4}=\frac{l+1}{l}•\frac{m+1}{m}$������12�֣�
������5lm-4l=4m+4��$l=\frac{4m+4}{5m-4}$����$\frac{4m+4}{5m-4}��1$����1��m��8������14�֣�
һһ�������$\left\{\begin{array}{l}m=1\\ l=8\end{array}\right.$��$\left\{\begin{array}{l}m=2\\ l=2\end{array}\right.$��$\left\{\begin{array}{l}m=3\\ l=\frac{16}{11}\end{array}\right.$��$\left\{\begin{array}{l}m=4\\ l=\frac{5}{4}\end{array}\right.$��$\left\{\begin{array}{l}m=5\\ l=\frac{8}{7}\end{array}\right.$��$\left\{\begin{array}{l}m=6\\ l=\frac{14}{13}\end{array}\right.$��$\left\{\begin{array}{l}m=7\\ l=\frac{32}{31}\end{array}\right.$��$\left\{\begin{array}{l}m=8\\ l=1\end{array}\right.$
��l��m�����Դ���l=1��m=8��������������16�֣�
���� ���⿼���������е�ǰn�����ͨ�ʽ�Լ��Ȳ�����ͨ�ʽ�����ã��ؼ�����ȷ���{an}ͨ�ʽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
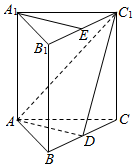 ��ͼ����������ABC-A1B1C1�У�D��BC���е㣮
��ͼ����������ABC-A1B1C1�У�D��BC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3�� | B�� | 9�� | C�� | $\frac{9��}{2}$ | D�� | $\frac{7��}{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com