练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    不全相等的五个数a、b、c、m、n具有关系如下：a、b、c成等比数列，a、m、b和b、n、c都成等差数列，则
    a
    m
    +
    c
    n
    =（　　）
    A、-2B、0C、2D、不能确定
    考点：等比数列的通项公式,等差数列的通项公式
    专题：等差数列与等比数列
    分析：由已知得2m=a+b，2n=b+c，b2=ac，从而
    a
    m
    +
    c
    n
    =
    an+cm
    mn
    =
    2(ab+ac+ac+bc)
    (a+b)(b+c)
    =
    2(ab+2b2+bc)
    ab+2b2+bc
    =2．
    解答： 解：由已知得2m=a+b，2n=b+c，b2=ac，
    ∴
    a
    m
    +
    c
    n
    =
    an+cm
    mn

    =
    1
    mn
    [
    a(b+c)
    2
    +
    c(a+b)
    2
    ]
    =
    2(ab+ac+ac+bc)
    (a+b)(b+c)

    =
    2(ab+2b2+bc)
    ab+2b2+bc
    =2．
    故选：C．
    点评：本题考查代数和的求法，是基础题，解题时要认真审题，注意等差数列和等比数列的性质的合理运用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

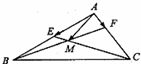    在平面向量中有如下定理：设点O、P、Q、R为同一平面内的点，则P、Q、R三点共线的充要条件是：存在实数t，使
    OP
    =（1-t）
    OQ
    +t
    OR
    ．试利用该定理解答下列问题：
    如图，在△ABC中，点E为AB边的中点，点F在AC边上，且CF=2FA，BF交CE于点M，设
    AM
    =x
    AE
    +y
    AF
    ，则x+y=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    曲线y=e2x+3（e为自然对数的底数）在x=0处的切线方程为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某几何体的三视图如图，若该几何体的所有顶点都在一个球面上，则该球面的表面积为（　　）
    A、4π
    B、
    28
    3
    π
    C、
    44
    3
    π
    D、20π

    查看答案和解析>>

    科目：高中数学 来源： 题型：

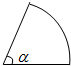    现要用篱笆围成一个面积为S扇形菜园（如图所示），问要使这个菜园所用篱笆最短，则这个扇形的半径和圆心角各为（　　）
    A、
    		S
    和1
    B、2
    		S
    和2
    C、
    		S
    和2
    D、2
    		S
    和1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若复数z满足z（2+i）=5i-10，则|z|=（　　）
    A、25
    B、5
    		5
    C、
    		5
    D、5

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    函数f（x）=2sin（ωx+φ）（ω＞0，
    π
    2
    ＜φ＜π）的部分图象如图，其中A、B两点之间的距离为5，则f（-1）=（　　）
    A、2
    B、
    		3
    C、-
    		3
    D、-2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知点M（2，-3），N（-3，-2），直线ax+y-1-a=0与线段MN相交，则实数a的取值范围是（　　）
    A、-
    3
    4
    ≤a≤4
    B、-4≤a≤
    3
    4
    C、a≤-
    3
    4
    或a≥4
    D、a≤-4或a≥
    3
    4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    函数f（x）=
    1
    ax2+4ax+3
    的定义域为R，则实数a的取值范围是（　　）
    A、[0，
    3
    4
    ）
    B、（0，
    3
    4
    ）
    C、（
    3
    4
    ，+∞）
    D、（-∞，0）

    查看答案和解析>>

    同步练习册答案