设{an}是公比不为1的等比数列，其前n项和为Sn，且a5，a3，a4成等差数列．
(1) 求数列{an}的公比；
(2) 证明：对任意k∈N＋，Sk＋2，Sk，Sk＋1成等差数列．
优加精卷系列答案科目：高中数学 来源： 题型：
从2007年1月2日起，每年1月2日到银行存入一万元定期储蓄，若年利率为p，且保持不变，并约定每年到期存款均自动转为新一年的定期存款，到2013年1月1日将所有存款和利息全部取回，则可取回的钱的总数为________万元．
查看答案和解析>>
科目：高中数学 来源： 题型：
已知各项均为正数的等比数列{an}的公比为q，且0＜q＜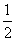
.
(1) 在数列{an}中是否存在三项，使其成等差数列？说明理由；
(2) 若a1＝1，且对任意正整数k，ak－(ak＋1＋ak＋2)仍是该数列中的某一项．
(ⅰ) 求公比q；
(ⅱ) 若bn＝－logan＋1(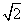
＋1)，Sn＝b1＋b2＋…＋bn，Tr＝S1＋S2＋…＋Sn，试用S2 011表示T2 011.
查看答案和解析>>
科目：高中数学 来源： 题型：
甲、乙两大超市同时开业，第一年的全年销售额均为a万元，由于经营方式不同，甲超市前n年的总销售额为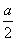
(n2－n＋2)万元，乙超市第n年的销售额比前一年销售额多
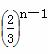a万元．
(1) 设甲、乙两超市第n年的销售额分别为an、bn, 求an、bn的表达式；
(2) 若其中某一超市的年销售额不足另一超市的年销售额的50%，则该超市将被另一超市收购，判断哪一超市有可能被收购？如果有这种情况，将会出现在第几年？
查看答案和解析>>
科目：高中数学 来源： 题型：
设数列{an}的前n项和为Sn.已知a1＝1，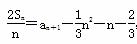
，n∈N*.
(1) 求a2的值；
(2) 求数列{an}的通项公式；
(3) 证明：对一切正整数n，有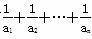
<
.
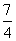查看答案和解析>>
科目：高中数学 来源： 题型：
在△ABC中，
(1) 若a＝4，B＝30°，C＝105°，则b＝________．
(2) 若b＝3，c＝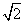
，C＝45°，则a＝________．
(3) 若AB＝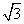
，BC＝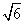
，C＝30°，则∠A＝________．
查看答案和解析>>
科目：高中数学 来源： 题型：
已知函数f(x)＝Asin
，x∈R，A>0，0<φ<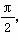
，y＝f(x)的部分图象如图所示，P、Q分别为该图象的最高点和最低点，点P的坐标为(1，A)．
(1) 求f(x)的最小正周期及φ的值；
(2) 若点R的坐标为(1，0)，∠PRQ＝
，求A的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
；
.