
分析 分别求出p,q为真时的x的范围,根据集合的包含关系得到关于m的不等式组,解出即可.
解答 解:由p:|1-$\frac{x-1}{3}$|≥2,解得:x≤-2或x≥10,
故¬p:-2<x<10,记为集合A={x|-2<x<10},
由q:x2-2x+1-m2≥0(m>0),
解得:x≤1-m或x≥1+m,
故¬q:1-m<x<1+m,
记为集合B={x|1-m<x<1+m},
∵¬p是¬q的必要不充分条件,
∴B?A,
∴$\left\{\begin{array}{l}{1-m≥-2}\\{1+m≤10}\\{m>0}\end{array}\right.$,解得:0<m≤3,
故实数m的取值范围为(0,3].
点评 本题考查了充分必要条件,考查集合的包含关系以及不等式问题,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-4,+∞) | B. | (-2,+∞) | C. | [-4,-2) | D. | [-4,-2)∪(-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2,-1} | B. | {0,1} | C. | {-1,0,1} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
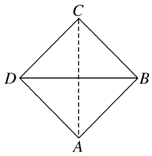 已知正四面体(所有棱长都相等的三棱锥)的俯视图如图所示,其中四边形ABCD是边长为$\sqrt{2}$cm的正方形,则这个正四面体的主视图的面积为( )cm2.
已知正四面体(所有棱长都相等的三棱锥)的俯视图如图所示,其中四边形ABCD是边长为$\sqrt{2}$cm的正方形,则这个正四面体的主视图的面积为( )cm2.| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{2}]$ | B. | (0,1) | C. | $(\frac{1}{2},1)$ | D. | $[\frac{1}{2},1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
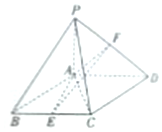 如图,四棱锥P-ABCD中,底面ABCD为菱形,∠ABC=60°,PA⊥平面ABCD,AB=2,PA=$\frac{{2\sqrt{3}}}{3}$,E为BC中点,F在棱PD上,AF⊥PD,点B到平面AEF的距离为$\frac{\sqrt{3}}{2}$.
如图,四棱锥P-ABCD中,底面ABCD为菱形,∠ABC=60°,PA⊥平面ABCD,AB=2,PA=$\frac{{2\sqrt{3}}}{3}$,E为BC中点,F在棱PD上,AF⊥PD,点B到平面AEF的距离为$\frac{\sqrt{3}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com