
����Ŀ��[ѡ��4-4������ϵ���������]����ƽ����ȡ��һ��������ϵ���Լ�����Ϊֱ������ϵ��x��������ᣬ�Ԧ�= ![]() ��������Ϊy��������ᣬ�Լ���Ϊ����ԭ�㣬���ȵ�λ���䣬����ֱ������ϵ����֪����C��ֱ�����귽��Ϊx2+y2=2��ֱ��l�IJ�������
��������Ϊy��������ᣬ�Լ���Ϊ����ԭ�㣬���ȵ�λ���䣬����ֱ������ϵ����֪����C��ֱ�����귽��Ϊx2+y2=2��ֱ��l�IJ������� ![]() ��tΪ��������
��t��������
��1��д��ֱ��l����ͨ����������C�ļ����귽�̣�
��2����ƽ���������任���������ʽΪ ![]() ����C�ڴ˱任�µõ�����C'�ķ��̣���������C���ڽӾ��ε���������
����C�ڴ˱任�µõ�����C'�ķ��̣���������C���ڽӾ��ε���������
���𰸡�
��1���⣺��ֱ��l�IJ������� ![]() ��tΪ����������ȥ��������Ϊֱ�����귽��Ϊ 2x+y��2=0��
��tΪ����������ȥ��������Ϊֱ�����귽��Ϊ 2x+y��2=0��
����C��ֱ�����귽��Ϊx2+y2=2���� ��2=2���� ��= ![]() ��
��
��2���⣺��ƽ���������任���������ʽΪ ![]() ��
��
����C�ڴ˱任�µõ�����C'�ķ���Ϊ ![]() +Y2=2����
+Y2=2���� ![]() +
+ ![]() =1��
=1��
����C'�IJ�������Ϊ 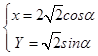 ��������Բ�ĶԳ��ԣ����ߵ��ڽӾ��ε����Ϊ4|XY|=8|sin2��|��
��������Բ�ĶԳ��ԣ����ߵ��ڽӾ��ε����Ϊ4|XY|=8|sin2��|��
�ʵ���= ![]() ʱ�����ߵ��ڽӾ��ε�������Ϊ8��
ʱ�����ߵ��ڽӾ��ε�������Ϊ8��
����������1����ֱ��l�IJ���������ȥ��������Ϊֱ�����귽�̣�����C��ֱ�����귽��Ϊx2+y2=2������2=2������ɵý������2�����������C�ڴ˱任�µõ�����C'�ķ���Ϊ ![]() +Y2=2�����������C'�IJ�������Ϊ
+Y2=2�����������C'�IJ�������Ϊ ![]() ��������Բ�ĶԳ��ԣ����ߵ��ڽӾ��ε����Ϊ4|XY|=8|sin2��|���ɴ˿ɵ����ߵ��ڽӾ��ε�������ֵ��
��������Բ�ĶԳ��ԣ����ߵ��ڽӾ��ε����Ϊ4|XY|=8|sin2��|���ɴ˿ɵ����ߵ��ڽӾ��ε�������ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ԲC�� ![]() =1��a��b��0������Բ����ԭ��O���뾶Ϊ
=1��a��b��0������Բ����ԭ��O���뾶Ϊ ![]() ��Բ����ԲC�ġ�Բ��������ԲC��һ������ΪF��
��Բ����ԲC�ġ�Բ��������ԲC��һ������ΪF�� ![]() ��0����������ϵ�һ���˵㵽F�ľ���Ϊ
��0����������ϵ�һ���˵㵽F�ľ���Ϊ ![]() ��
��
��������ԲC�ķ��̺��䡰Բ�����̣�
����P����ԲC�ġ�Բ���ϵĶ��㣬����P����Բ������l1 �� l2����Բ���ڵ�M��N��
����������PΪ��Բ����y��������Ľ���ʱ����ֱ��l1 �� l2�ķ��̲�֤��l1��l2��
��������֤���߶�MN�ij�Ϊ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������a��b��ʹ��x��R��f��x+a����f��x��+b����������f��x��Ϊ����������������������������������f��x��=x2+x+1���� ![]() ����f��x��=sin��x2���������ǡ��������������ǣ� ��
����f��x��=sin��x2���������ǡ��������������ǣ� ��
A.�٢ڢ�
B.�ڢ�
C.�٢�
D.��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ�������������ȱˮ�Ĺ��ң�ij������Ϊ�˹��������Լ��ˮ���ƻ���������������ˮ�շѷ�������ȷ��һ������������ˮ����x���֣���һλ���������ˮ��������x�IJ��ְ�ƽ���շѣ�����x�IJ��ְ�����շѣ�Ϊ���˽������ˮ�����ͨ�������������ij��100λ����ÿ�˵��¾���ˮ������λ���֣��������ݰ���[0��0.5����[0.5��1��������[4��4.5���ֳ�9�飬�Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
������ֱ��ͼ��a��ֵ��
��������Ƶ����Ϊ���ʣ��Ӹó��о����������ȡ3�ˣ�����3�����¾���ˮ��������3�ֵ�����ΪX����X�ķֲ�������ѧ������
��������������ϣ��ʹ85%�ľ���ÿ�µ���ˮ����������x���֣�������x��ֵ����ȷ��0.01������˵�����ɣ�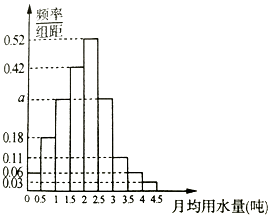
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ִ����ͼ��ʾ�ij����ͼ��������Ľ����8�����жϿ���m��ȡֵ��Χ�ǣ� �� 
A.��30��42]
B.��42��56]
C.��56��72]
D.��30��72��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��֪ ![]() =��2��sinx��sinx+cosx����
=��2��sinx��sinx+cosx���� ![]() =��
=�� ![]() cosx���ˣ�sinx��cosx�������ˣ�0��������f��x��=
cosx���ˣ�sinx��cosx�������ˣ�0��������f��x��= ![]()
![]() �����ֵΪ2��
�����ֵΪ2��
��1������f��x���ĵ����ݼ����䣻
��2���ڡ�ABC�У��ڽ�A��B��C�ĶԱ߷ֱ�Ϊa��b��c��cosA= ![]() ����f��A����m��0���������ʵ��m��ȡֵ��Χ��
����f��A����m��0���������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��P��ԲC��x2+y2=4�ϣ���QΪP��x���ϵ�ͶӰ���ҵ�N���� ![]() ���趯��N�Ĺ켣Ϊ����E��
���趯��N�Ĺ켣Ϊ����E��
��1��������E�ķ��̣�
��2����A��B������E�����㣬��|AB|=2��OΪ����ԭ�㣬���AOB����������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������Ͷ�����Σ���һ�γ��ֵĵ�����Ϊa���ڶ��γ��ֵĵ�����Ϊb��������ֱ��l1��ax+by=2��l2��x+2y=2ƽ�еĸ���ΪP1 �� �ཻ�ĸ���ΪP2 �� ���P��36P1 �� 36P2����ԲC��x2+y2=1098��λ�ù�ϵ�ǣ� ��
A.��P��ԲC��
B.��P��ԲC��
C.��P��ԲC��
D.����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() cos2x��2cos2��x+
cos2x��2cos2��x+ ![]() ��+1��
��+1��
������f��x���ĵ����������䣻
������f��x��������[0�� ![]() ]�ϵ���ֵ��
]�ϵ���ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com