Question

14．如图，已知椭圆$\frac{x^2}{3}$+y²=1的右顶点为A，上顶点和下顶点分别是点B和C，点P是直线L：y=-2上的一个动点（P不在y轴上），直线PC交椭圆于另一点M．
（1）当直线PM过点A时，求△ABP的面积；
（2）求证：△MBP为直角三角形；
（3）以A，B为焦点，且过点P的椭圆有无数个，求这些椭圆的离心率的最大值．

Answer 1

分析 （1）直线AC的方程易求，从而可得P点坐标，运用点到直线的距离公式和两点的距离公式，从而△ABP的面积可求；
（2）设P（m，-2）（m≠0），求得PM的斜率，联立直线PM和椭圆方程，可得M的坐标，利用直线PB与BM斜率之积为-1可证；
（3）点B关于直线y=-2的对称点B′可求，连AB′与y=-2的交点即为P，求得AB'的长，即为PA+PB的长，由椭圆定义和离心率公式，可得最大值．

解答 解：（1）由椭圆的方程$\frac{{x}^{2}}{3}$+y²=1，可得a=$\sqrt{3}$，b=1，c=$\sqrt{2}$，
即有B（0，1），C（0，-1），A（$\sqrt{3}$，0），
直线PM即PC：$\frac{x}{\sqrt{3}}$-y=1，即为x-$\sqrt{3}$y-$\sqrt{3}$=0，
由y=-2，代入上式可得x=-$\sqrt{3}$，
P（-$\sqrt{3}$，-2）到直线BA：x+$\sqrt{3}$y-$\sqrt{3}$=0的距离为d=$\frac{|-\sqrt{3}-2\sqrt{3}-\sqrt{3}|}{\sqrt{1+3}}$=2$\sqrt{3}$，
即有S_△ABP=$\frac{1}{2}$BA•d=$\frac{1}{2}$•2•2$\sqrt{3}$=2$\sqrt{3}$；
（2）证明：设P（m，-2）（m≠0），k_PM=$\frac{-1-（-2）}{0-m}$=-$\frac{1}{m}$，
PM：y=-$\frac{1}{m}$x-1，代入椭圆方程可得（3+m²）x²+6mx=0，
解得M（-$\frac{6m}{3+{m}^{2}}$，$\frac{3-{m}^{2}}{3+{m}^{2}}$），
k_PB=$\frac{1-（-2）}{0-m}$=-$\frac{3}{m}$，k_BM=$\frac{\frac{3-{m}^{2}}{3+{m}^{2}}-1}{-\frac{6m}{3+{m}^{2}}-0}$=$\frac{m}{3}$，
则k_PBk_BM=-1，即PB⊥BM，
即有△MBP为直角三角形；
（3）设B关于直线y=-2的对称点为B'，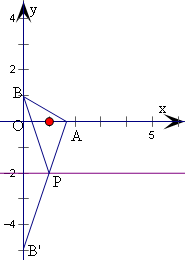
由B（0，1），可得B'（0，-5），
连接AB'，交直线y=-2即为P，
则P到A，B的距离之和最小，
且为|AB'|=$\sqrt{3+25}$=2$\sqrt{7}$，
|AB|=$\sqrt{3+1}$=2，
由2$\sqrt{7}$＞2，可知以A，B为焦点的椭圆经过P，
此时椭圆的离心率取得最大，
且为e=$\frac{2c}{2a}$=$\frac{2}{2\sqrt{7}}$=$\frac{\sqrt{7}}{7}$．

点评 本题考查椭圆的定义、方程和性质，考查直线和椭圆联立，以及点关于直线对称的求法，两直线垂直的条件，考查化简整理的运算能力，属于中档题．