
分析 依题意F(1,0),设直线MN方程为x=my+1.将直线MN的方程与抛物线的方程联立,得y2-4my-4=0.由此能够求出直线的斜率,可得|MF|.
解答 解:依题意F(1,0),设直线MN方程为x=my+1.
将直线MN的方程与抛物线的方程联立,消去x得y2-4my-4=0.
设M(x1,y1),N(x2,y2),所以 y1+y2=4m,y1y2=-4.
x1x2=$\frac{1}{16}$(y1y2)2=1①
因为|MD|=2|NF|,|DF|=1,
所以 x1=2x2+2②
联立①和②,解得x1=1+$\sqrt{3}$(负的舍去),
|MF|=x1+1=2+$\sqrt{3}$.
故答案为:2+$\sqrt{3}$.
点评 本题考查直线斜率的求法,抛物线的简单性质的应用,解题时要认真审题,仔细解答,注意挖掘题设中的条件,合理地进行等价转化.


科目:高中数学 来源: 题型:选择题
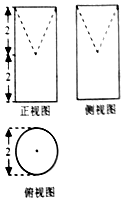
 祖冲之之子祖暅是我国南北朝时代伟大的科学家,他在实践的基础上提出了体积计算的原理:“幂势既同,则积不容异”.意思是,如果两个等高的几何体在同高处截得的截面面积恒等,那么这两个几何体的体积相等.此即祖暅原理.利用这个原理求球的体积时,需要构造一个满足条件的几何体,已知该几何体三视图如图所示,用一个与该几何体的下底面平行相距为h(0<h<2)的平面截该几何体,则截面面积为( )
祖冲之之子祖暅是我国南北朝时代伟大的科学家,他在实践的基础上提出了体积计算的原理:“幂势既同,则积不容异”.意思是,如果两个等高的几何体在同高处截得的截面面积恒等,那么这两个几何体的体积相等.此即祖暅原理.利用这个原理求球的体积时,需要构造一个满足条件的几何体,已知该几何体三视图如图所示,用一个与该几何体的下底面平行相距为h(0<h<2)的平面截该几何体,则截面面积为( )| A. | 4π | B. | πh2 | C. | π(2-h)2 | D. | π(4-h2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{\sqrt{2}}{8}$ | C. | $\frac{2\sqrt{6}}{5}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{2}}{3}$ | B. | $\sqrt{7}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某三棱锥的三视图如图所示,其中三个视图都是直角三角形,则该三棱锥外接球的体积为( )
某三棱锥的三视图如图所示,其中三个视图都是直角三角形,则该三棱锥外接球的体积为( )| A. | 2π | B. | $\sqrt{6}π$ | C. | 6π | D. | $4\sqrt{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (9+$\sqrt{5}$)π | B. | (9+2$\sqrt{5}$)π | C. | (10+$\sqrt{5}$)π | D. | (10+2$\sqrt{5}$)π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | 1 | C. | $\sqrt{5}$ | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com