
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 进行向量的数乘运算即可判断每个运算的正误,从而得出正确运算的个数.
解答 解:$①(-3)•2\overrightarrow{a}=-6\overrightarrow{a}$,该运算正确;
②$2(\overrightarrow{a}+\overrightarrow{b})-(2\overrightarrow{b}-\overrightarrow{a})=2\overrightarrow{a}+2\overrightarrow{b}-2\overrightarrow{b}+\overrightarrow{a}$=$3\overrightarrow{a}$,∴该运算正确;
③$(\overrightarrow{a}+2\overrightarrow{b})-(2\overrightarrow{b}+\overrightarrow{a})=\overrightarrow{a}+2\overrightarrow{b}-2\overrightarrow{b}-\overrightarrow{a}=\overrightarrow{0}$,是零向量,不是0,∴该运算错误;
∴运算正确的个数为2.
故选:C.
点评 考查向量的数乘运算,清楚零向量的表示为$\overrightarrow{0}$,而不是0.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
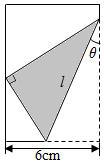 如图,将矩形纸片的右下角折起,使得该角的顶点落在矩形的左边上,那么折痕长度l取决于角θ的大小,探求l,θ之间的关系式,并导出用θ表示l的函数表达式.
如图,将矩形纸片的右下角折起,使得该角的顶点落在矩形的左边上,那么折痕长度l取决于角θ的大小,探求l,θ之间的关系式,并导出用θ表示l的函数表达式.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com