
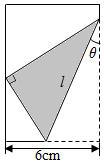
 如图,将矩形纸片的右下角折起,使得该角的顶点落在矩形的左边上,那么折痕长度l取决于角θ的大小,探求l,θ之间的关系式,并导出用θ表示l的函数表达式.
如图,将矩形纸片的右下角折起,使得该角的顶点落在矩形的左边上,那么折痕长度l取决于角θ的大小,探求l,θ之间的关系式,并导出用θ表示l的函数表达式. 分析 根据图形判断直角三角形,利用直角三角形求解AE=GEcos2θ=lsinθcos2θ,由AE+BE=lsinθcos2θ+lsinθ=6,求解即可.
解答 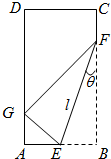 解:由已知及对称性知,GF=BF=lcosθ,GE=BE=lsinθ,
解:由已知及对称性知,GF=BF=lcosθ,GE=BE=lsinθ,
又∠GEA=∠GFB=2θ,
∴AE=GEcos2θ=lsinθcos2θ,
又由AE+BE=lsinθcos2θ+lsinθ=6得:l=$\frac{6}{sinθ(_1+cos2θ)}$
BF=lcosθ=$\frac{6}{sinθ(_1+cos2θ)}$•cosθ=$\frac{6}{sin2θ}$≤BC
点评 本题考查了矩形的对折问题、直角三角形的边角关系、倍角公式、三角函数的单调性、利用导数研究函数的单调性极值与最值,考查了推理能力与计算能力,属于难题


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com