
分析 (Ⅰ)由题意和余弦定理可得a2+b2-c2=ab,再由余弦定理可得cosC,可得角C;
(Ⅱ)由已知数据和余弦定理可解得ab的值,代入三角形的面积公式可得.
解答 解:(Ⅰ)在△ABC中,由2ccosB=2a-b和余弦定理可得$2c\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=2a-b$,
∴a2+b2-c2=ab,∴$cosC=\frac{{{a^2}+{b^2}-{c^2}}}{2ab}=\frac{1}{2}$,
又C∈(0,π),∴$C=\frac{π}{3}$;
(Ⅱ)∵$C=\frac{π}{3}$,$c=\sqrt{3}$,∴由余弦定理可得a2+b2-ab=3,
又∵b-a=1,∴a2+a-2=0,∴a=1或a=-2(舍去),
∴a=1,b=2,$c=\sqrt{3}$,
∴△ABC的面积S=$\frac{1}{2}$absinC=$\frac{\sqrt{3}}{2}$
点评 本题考查正余弦定理解三角形,涉及三角形的面积公式,属基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k>5 | B. | 5<k<9 | C. | k<5 | D. | k>9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -log2(2-$\sqrt{2}$) | C. | $\frac{1}{2}$ | D. | log2(2-$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,1} | B. | {-1} | C. | {1} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
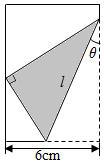 如图,将矩形纸片的右下角折起,使得该角的顶点落在矩形的左边上,那么折痕长度l取决于角θ的大小,探求l,θ之间的关系式,并导出用θ表示l的函数表达式.
如图,将矩形纸片的右下角折起,使得该角的顶点落在矩形的左边上,那么折痕长度l取决于角θ的大小,探求l,θ之间的关系式,并导出用θ表示l的函数表达式.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com