
分析 (Ⅰ)由已知及三角形内角和定理,两角和与差的正弦函数公式化简可得2sinAcosB=$\sqrt{2}$sinA,由于sinA≠0,即可解得cosB的值,结合范围B∈(0,π),即可求得B的值.
(Ⅱ)由余弦定理及基本不等式可得:a2+c2-$\sqrt{2}$ac=4,且ac≤$\frac{{a}^{2}+{c}^{2}}{2}$,从而可得4≥(1-$\frac{\sqrt{2}}{2}$)(a2+c2),即可解得a2+c2的最大值.
解答 (本题满分为12分)
解:(Ⅰ)在△ABC中,∵由已知及C=π-(A+B)可得:
sin(A-B)+sinC=sin(A-B)+sin(A+B)
=sinAcosB-cosAsinB+sinAcosB+cosAsinB
=2sinAcosB=$\sqrt{2}$sinA…3分
∵A是三角形的内角,sinA≠0,
∴cosB=$\frac{\sqrt{2}}{2}$…4分
∴由B∈(0,π),可得B=$\frac{π}{4}$…5分
(Ⅱ)∵由余弦定理可得:a2+c2-$\sqrt{2}$ac=4,且ac≤$\frac{{a}^{2}+{c}^{2}}{2}$,…7分
∴4=a2+c2-$\sqrt{2}$ac≥(a2+c2)-$\frac{\sqrt{2}}{2}$(a2+c2)=(1-$\frac{\sqrt{2}}{2}$)(a2+c2),…9分
∴a2+c2≤$\frac{4}{1-\frac{\sqrt{2}}{2}}$=8$+4\sqrt{2}$(当且仅当a=c时,等号成立),…11分
∴当A=C=$\frac{3π}{8}$时,a2+c2的最大值是8$+4\sqrt{2}$…12分
点评 本题主要考查了三角形内角和定理,两角和与差的正弦函数公式,余弦定理及基本不等式在解三角形中的应用,考查了计算能力和转化思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{144}$+$\frac{{y}^{2}}{108}$=1 | B. | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{32}$=1 | C. | $\frac{{x}^{2}}{32}$+$\frac{{y}^{2}}{36}$=1 | D. | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{27}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |x+4| | B. | |2-x| | C. | 2+|x+1| | D. | 3-|x+1| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
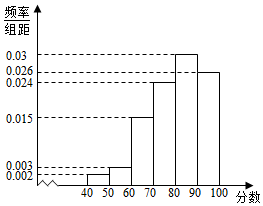 作为市政府为民办实事之一的公共自行车建设工作已经基本完成了,相关部门准备对该项目进行验收,验收的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,在公共自行车自助点随机访问了前来使用的100名市民,并根据这100名市民对该项目满意程度的评分(满分100分),绘制了如图频率分布直方图:
作为市政府为民办实事之一的公共自行车建设工作已经基本完成了,相关部门准备对该项目进行验收,验收的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,在公共自行车自助点随机访问了前来使用的100名市民,并根据这100名市民对该项目满意程度的评分(满分100分),绘制了如图频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com