
分析 (1)把直线l的方程化为m(2x+y-7)+(x+y-4)=0,令$\left\{\begin{array}{l}{2x+y-7=0}\\{x+y-4=0}\end{array}\right.$,求出方程组的解即得;
(2)根据圆C的圆心到定点A的距离d<r,得出A点在圆C内,直线l与圆C相交;
(3)求m=0时圆心C到直线l的距离,利用勾股定理求出直线l被圆C所截得的弦长即可.
解答 解:(1)证明:直线l的方程可化为:
m(2x+y-7)+(x+y-4)=0,
令$\left\{\begin{array}{l}{2x+y-7=0}\\{x+y-4=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$,
∴直线l恒过定点A(3,1);
(2)圆C:(x-1)2+(y-2)2=25的圆心C(1,2),半径r=5,
点A(3,1)与圆心C(1,2)的距离d=$\sqrt{{(3-1)}^{2}{+(1-2)}^{2}}$=$\sqrt{5}$<5=r,
∴A点在圆C内,即直线l与圆C相交;
(3)当m=0时,直线l的方程为x+y-4=0,
由圆心C(1,2)到直线l的距离为d′=$\frac{|1+2-4|}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
半径r=5,
∴直线l被圆C所截得的弦长为2$\sqrt{{r}^{2}{-d′}^{2}}$=2$\sqrt{{5}^{2}{-(\frac{\sqrt{2}}{2})}^{2}}$=7$\sqrt{2}$.
点评 本题考查了直线与圆相交的性质,以及直线恒过定点的问题,也考查了直线被圆所截得弦长的计算问题,是综合性题目.


科目:高中数学 来源: 题型:选择题
| x | 16 | 17 | 18 | 19 |
| y | 50 | 34 | 41 | 31 |
| A. | 26个 | B. | 27个 | C. | 28个 | D. | 29个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,1} | B. | {-1} | C. | {1} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
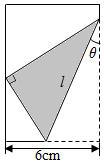 如图,将矩形纸片的右下角折起,使得该角的顶点落在矩形的左边上,那么折痕长度l取决于角θ的大小,探求l,θ之间的关系式,并导出用θ表示l的函数表达式.
如图,将矩形纸片的右下角折起,使得该角的顶点落在矩形的左边上,那么折痕长度l取决于角θ的大小,探求l,θ之间的关系式,并导出用θ表示l的函数表达式.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com