
Ζ÷Έω ΗυΨίœρΝΩ¥Ι÷±”κœρΝΩ ΐΝΩΜΐΒΡΙΊœΒΩ…ΒΟΘ®$\overrightarrow{a}$+$\overrightarrow{b}$Θ©•Θ®$\overrightarrow{a}$-$\overrightarrow{b}$Θ©=0Θ§Ι |$\overrightarrow{b}$|=|$\overrightarrow{a}$|Θ°
Ϋβ¥π ΫβΘΚΓΏΘ®$\overrightarrow{a}$+$\overrightarrow{b}$Θ©ΓΆΘ®$\overrightarrow{a}$-$\overrightarrow{b}$Θ©Θ§
ΓύΘ®$\overrightarrow{a}$+$\overrightarrow{b}$Θ©•Θ®$\overrightarrow{a}$-$\overrightarrow{b}$Θ©=0Θ§
Φ¥${\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}=0$Θ§
Γύ|$\overrightarrow{b}$|=|$\overrightarrow{a}$|=$\sqrt{{1}^{2}+{3}^{2}}=\sqrt{10}$Θ°
Ι ¥πΑΗΈΣΘΚ$\sqrt{10}$Θ°
ΒψΤά ±ΨΧβΩΦ≤ιΝΥΤΫΟφœρΝΩΒΡ ΐΝΩΜΐ‘ΥΥψΘ§ΡΘ≥ΛΦΤΥψΘ§ τ”ΎΜυ¥ΓΧβΘ°


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| x | 16 | 17 | 18 | 19 |
| y | 50 | 34 | 41 | 31 |
| AΘ° | 26Ηω | BΘ° | 27Ηω | CΘ° | 28Ηω | DΘ° | 29Ηω |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 0 | BΘ° | 2 | CΘ° | 3 | DΘ° | 4 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | kΘΨ5 | BΘ° | 5ΘΦkΘΦ9 | CΘ° | kΘΦ5 | DΘ° | kΘΨ9 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
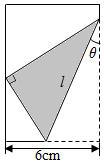 »γΆΦΘ§ΫΪΨΊ–Έ÷ΫΤ§ΒΡ”“œ¬Ϋ«’έΤπΘ§ ΙΒΟΗΟΫ«ΒΡΕΞΒψ¬δ‘ΎΨΊ–ΈΒΡΉσ±Ώ…œΘ§Ρ«Ο¥’έΚέ≥ΛΕ»l»ΓΨω”ΎΫ«Π»ΒΡ¥σ–ΓΘ§ΧΫ«σlΘ§Π»÷°ΦδΒΡΙΊœΒ ΫΘ§≤ΔΒΦ≥ω”ΟΠ»±μ ΨlΒΡΚ· ΐ±μ¥ο ΫΘ°
»γΆΦΘ§ΫΪΨΊ–Έ÷ΫΤ§ΒΡ”“œ¬Ϋ«’έΤπΘ§ ΙΒΟΗΟΫ«ΒΡΕΞΒψ¬δ‘ΎΨΊ–ΈΒΡΉσ±Ώ…œΘ§Ρ«Ο¥’έΚέ≥ΛΕ»l»ΓΨω”ΎΫ«Π»ΒΡ¥σ–ΓΘ§ΧΫ«σlΘ§Π»÷°ΦδΒΡΙΊœΒ ΫΘ§≤ΔΒΦ≥ω”ΟΠ»±μ ΨlΒΡΚ· ΐ±μ¥ο ΫΘ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com