
分析 (I)椭圆C的离心率为$\frac{{\sqrt{3}}}{2}$,$P(\sqrt{2},\frac{{\sqrt{2}}}{2})$在椭圆C上.可得$\frac{c}{a}=\frac{\sqrt{3}}{2}$,$\frac{2}{{a}^{2}}+\frac{1}{2{b}^{2}}$=1,a2=b2+c2,联立解得即可得出.
(II))(i)证明:当l⊥x轴时,设M(x0,y0),N(x0,-y0),则$\frac{{x}_{0}^{2}}{4}$+${y}_{0}^{2}$=1,由kOM•kON=-$\frac{b^2}{a^2}$,可得$\frac{{y}_{0}}{{x}_{0}}×\frac{-{y}_{0}}{{x}_{0}}$=-$\frac{1}{4}$,联立解得即可得出.
当l与x轴不垂直时,设直线l的方程为:y=kx+m,M(x1,y1),N(x2,y2),与椭圆方程联立化为:(1+4k2)x2+8kmx+4m2-4=0,△>0,可得1+4k2>m2.利用根与系数的关系可得|MN|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$.由kOM•kON=-$\frac{b^2}{a^2}$,可得$\frac{{y}_{1}}{{x}_{1}}•\frac{{y}_{2}}{{x}_{2}}$=-$\frac{1}{4}$,化为4(kx1+m)(kx2+m)+x1x2=0,把根与系数的关系代入可得:2m2=1+4k2.把m2=$\frac{1+4{k}^{2}}{2}$代入|MN|,可得|MN|=$\frac{2\sqrt{2(1+{k}^{2})}}{\sqrt{1+4{k}^{2}}}$,原点O到直线l的距离d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$.即可得出.S△MON=$\frac{1}{2}$|MN|d=1为定值.
(ii)当l⊥x轴时,由(i)可得:$\overrightarrow{OM}•\overrightarrow{ON}$=${x}_{0}^{2}-{y}_{0}^{2}$.当l与x轴不垂直时,可得:$\overrightarrow{OM}•\overrightarrow{ON}$=x1x2+y1y2=x1x2+(kx1+m)(kx2+m)=(1+k2)x1x2+mk(x1+x2)+m2=$\frac{5{m}^{2}-4{k}^{2}-4}{1+4{k}^{2}}$.把m2=$\frac{1+4{k}^{2}}{2}$代入$\overrightarrow{OM}•\overrightarrow{ON}$,化简整理即可得出.
解答 解:(I)∵椭圆C的离心率为$\frac{{\sqrt{3}}}{2}$,$P(\sqrt{2},\frac{{\sqrt{2}}}{2})$在椭圆C上.∴$\frac{c}{a}=\frac{\sqrt{3}}{2}$,$\frac{2}{{a}^{2}}+\frac{1}{2{b}^{2}}$=1,a2=b2+c2,联立解得a=2,b=1,c=$\sqrt{3}$,∴椭圆C的标准方程为$\frac{{x}^{2}}{4}$+y2=1.
(II)(i)证明:当l⊥x轴时,设M(x0,y0),N(x0,-y0),则$\frac{{x}_{0}^{2}}{4}$+${y}_{0}^{2}$=1,由kOM•kON=-$\frac{b^2}{a^2}$,可得$\frac{{y}_{0}}{{x}_{0}}×\frac{-{y}_{0}}{{x}_{0}}$=-$\frac{1}{4}$,联立解得:$\left\{\begin{array}{l}{{x}_{0}=\sqrt{2}}\\{{y}_{0}=±\frac{\sqrt{2}}{2}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{0}=-\sqrt{2}}\\{{y}_{0}=±\frac{\sqrt{2}}{2}}\end{array}\right.$,∴S△MON=$\frac{1}{2}×\sqrt{2}×\sqrt{2}$=1.
当l与x轴不垂直时,设直线l的方程为:y=kx+m,M(x1,y1),N(x2,y2),联立$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$,化为:(1+4k2)x2+8kmx+4m2-4=0,
△>0,可得1+4k2>m2.
∴x1+x2=$\frac{-8km}{1+4{k}^{2}}$,x1x2=$\frac{4{m}^{2}-4}{1+4{k}^{2}}$,
则|MN|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{(1+{k}^{2})[\frac{64{k}^{2}{m}^{2}}{(1+4{k}^{2})^{2}}-\frac{4(4{m}^{2}-4)}{1+4{k}^{2}}]}$=$\frac{4\sqrt{(1+{k}^{2})(1+4{k}^{2}-{m}^{2})}}{1+4{k}^{2}}$.
由kOM•kON=-$\frac{b^2}{a^2}$,可得$\frac{{y}_{1}}{{x}_{1}}•\frac{{y}_{2}}{{x}_{2}}$=-$\frac{1}{4}$,化为4(kx1+m)(kx2+m)+x1x2=0,即(1+4k2)x1x2+4mk(x1+x2)+4m2=0,
∴$\frac{(1+4{k}^{2})(4{m}^{2}-4)}{1+4{k}^{2}}$-$\frac{32{k}^{2}{m}^{2}}{1+4{k}^{2}}$+4m2=0,化为:2m2=1+4k2.
把m2=$\frac{1+4{k}^{2}}{2}$代入|MN|,可得|MN|=$\frac{2\sqrt{2(1+{k}^{2})}}{\sqrt{1+4{k}^{2}}}$,
原点O到直线l的距离d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$.
∴S△MON=$\frac{1}{2}$|MN|d=$\frac{\sqrt{2}}{\sqrt{1+4{k}^{2}}}$×|m|=$\frac{\sqrt{2}}{\sqrt{1+4{k}^{2}}}×\frac{\sqrt{1+4{k}^{2}}}{\sqrt{2}}$=1.
综上可得S△MON=1为定值.
(ii)当l⊥x轴时,由(i)可得:$\overrightarrow{OM}•\overrightarrow{ON}$=${x}_{0}^{2}-{y}_{0}^{2}$=$\frac{3}{2}$.
当l与x轴不垂直时,可得:$\overrightarrow{OM}•\overrightarrow{ON}$=x1x2+y1y2=x1x2+(kx1+m)(kx2+m)=(1+k2)x1x2+mk(x1+x2)+m2
=$\frac{(1+{k}^{2})(4{m}^{2}-4)}{1+4{k}^{2}}$-$\frac{8{m}^{2}{k}^{2}}{1+4{k}^{2}}$+m2=$\frac{5{m}^{2}-4{k}^{2}-4}{1+4{k}^{2}}$.
把m2=$\frac{1+4{k}^{2}}{2}$代入可得:$\overrightarrow{OM}•\overrightarrow{ON}$=$\frac{1}{2}×$$\frac{12{k}^{2}-3}{1+4{k}^{2}}$=$\frac{3}{2}$-$\frac{3}{1+4{k}^{2}}$.
由△>0,可得1+4k2>$\frac{1+4{k}^{2}}{2}$恒成立,∴k∈R.∴$\overrightarrow{OM}•\overrightarrow{ON}$∈$[-\frac{3}{2},\frac{3}{2})$.
综上可得:$\overrightarrow{OM}•\overrightarrow{ON}$∈$[-\frac{3}{2},\frac{3}{2}]$.
∴$\overrightarrow{OM}•\overrightarrow{ON}$的最小值为$-\frac{3}{2}$,最大值为$\frac{3}{2}$.
点评 本题考查了椭圆的标准方程及其性质、直线与圆相切的性质、一元二次方程的根与系数的关系、弦长公式、点到直线的距离公式、三角形面积计算公式、二次函数的单调性,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $f(x)=x-\frac{1}{x}$ | B. | f(x)=ex-1 | C. | $f(x)=x+\frac{4}{x}$ | D. | f(x)=tanx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
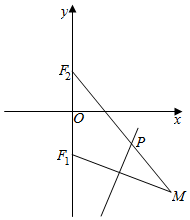 如图所示,点F1(0,-$\sqrt{2}$),F2(0,$\sqrt{2}$),动点M到点F2的距离是4,线段MF1的中垂线交MF2于点P.当点M变化时,则动点P的轨迹方程为( )
如图所示,点F1(0,-$\sqrt{2}$),F2(0,$\sqrt{2}$),动点M到点F2的距离是4,线段MF1的中垂线交MF2于点P.当点M变化时,则动点P的轨迹方程为( )| A. | $\frac{x^2}{4}+\frac{y^2}{2}=1$ | B. | $\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{2}$=1 | C. | x2+y2=1 | D. | $\frac{y^2}{4}-\frac{x^2}{2}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com