
分析 (1)根据绝对值的意义求出方程的根即可;(2)将f(x)写成分段函数的形式,从而求出f(x)的最小值,进而求出a的范围即可.
解答 解:(1)利用数形结合易知:方程|x-3|+|x+7|=16的两根为x1=-10,x2=6,
∴不等式f(x)=|x-3|+|x+7|<16的解集为(-10,6),
注:用零点分段法亦可.
(2)∵f(x)=|x-3|+|x+7|=$\left\{\begin{array}{l}{-2x-4,(x<-7)}\\{10,(-7≤x≤3)}\\{2x+4,(x>3)}\end{array}\right.$,
∴当x∈[-7,3]时,f(x)min=10;
∴依题意知:实数a的取值范围为a>10,即a∈(10,+∞).
点评 本题考查了绝对值的意义,函数的最值问题,考查分类讨论思想,是一道中档题.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
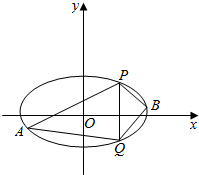 已知椭圆C的中心在原点,离心率等于$\frac{1}{2}$,它的一个短轴端点点恰好是抛物线$y=\frac{{\sqrt{3}}}{24}{x^2}$的焦点.
已知椭圆C的中心在原点,离心率等于$\frac{1}{2}$,它的一个短轴端点点恰好是抛物线$y=\frac{{\sqrt{3}}}{24}{x^2}$的焦点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某市气象部门对该市中心城区近4年春节期间(每年均统计春节假期的前7天)的空气污染指数进行了统计分析,且按是否燃放鞭炮分成两组,得到如图的茎叶图,根据国家最新标准,空气污染指数不超过100的表示没有雾霾,超过100的表示有雾霾.
某市气象部门对该市中心城区近4年春节期间(每年均统计春节假期的前7天)的空气污染指数进行了统计分析,且按是否燃放鞭炮分成两组,得到如图的茎叶图,根据国家最新标准,空气污染指数不超过100的表示没有雾霾,超过100的表示有雾霾.| 燃放 | 未燃放 | 合计 | |
| 有雾霾 | |||
| 无雾霾 | |||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com