
 ��֪��ԲC��������ԭ�㣬�����ʵ���$\frac{1}{2}$������һ������˵��ǡ����������$y=\frac{{\sqrt{3}}}{24}{x^2}$�Ľ��㣮
��֪��ԲC��������ԭ�㣬�����ʵ���$\frac{1}{2}$������һ������˵��ǡ����������$y=\frac{{\sqrt{3}}}{24}{x^2}$�Ľ��㣮���� ��1����C����Ϊ$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$��a��b��0�����������ʺ�����һ������˵��ǡ����������$y=\frac{{\sqrt{3}}}{24}{x^2}$�Ľ��㣬�����b��a���ɴ��������ԲC�ķ��̣�
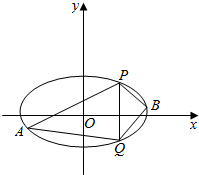
��2������ֱ��AB�ķ���Ϊy=$\frac{1}{2}x+t$��������Բ����x2+tx+t2-12=0���ɴ����ø����б�ʽ��Τ�ﶨ�����ҳ���ʽ��������ı���APBQ��������ֵ��
����ֱ��PA��б��Ϊk����PB��б��Ϊ-k��PA��ֱ�߷���Ϊy-3=k��x-2����������Բ���̵ã���3+4k2��x2+8��3-2k��kx+4��3-2k��2-48=0���Ӷ��õ�x1+x2��x1-x2���ɴ������ֱ��AB��б��Ϊ��ֵ��
��� �⣺��1������ԲC��������ԭ�㣬�����ʵ���$\frac{1}{2}$������һ������˵��ǡ����������$y=\frac{{\sqrt{3}}}{24}{x^2}$�Ľ��㣬
����C����Ϊ$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$��a��b��0����
��b=2$\sqrt{3}$����$\frac{c}{a}=\frac{1}{2}$��a2=b2+c2����a=4��
����ԲC�ķ���Ϊ$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$������4�֣�
��2������A��x1��y1����B��x2��y2����ֱ��AB�ķ���Ϊy=$\frac{1}{2}x+t$��
����$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$��������x2+tx+t2-12=0��
��=t2-4��t2-12����0�����-4��t��4��x1+x2=-t��${x}_{1}{x}_{2}={t}^{2}-12$��
�ı���APBQ�����S=$\frac{1}{2}��6��$|x1-x2|=3$\sqrt{48-3{t}^{2}}$��
��t=0ʱ��${S}_{max}=12\sqrt{3}$��
�ڵ�PA=PBʱ��PA��PB��б��֮��Ϊ0����ֱ��PA��б��Ϊk����PB��б��Ϊ-k��
PA��ֱ�߷���Ϊy-3=k��x-2����
����$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$���������3+4k2��x2+8��3-2k��kx+4��3-2k��2-48=0��
��2+1=$\frac{8��2k-3��k}{3+4{k}^{2}}$��
ͬ��2+2=$\frac{8��2k+3��k}{3+4{k}^{2}}$��x1+x2=$\frac{16{k}^{2}-12}{3+4{k}^{2}}$��x1-x2=$\frac{-48k}{3+4{k}^{2}}$��
�Ӷ�${k}_{AB}=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{k��{x}_{1}+{x}_{2}��-4k}{{x}_{1}-{x}_{2}}$=$\frac{1}{2}$����ֱ��AB��б��Ϊ��ֵ������13�֣�
���� ���⿼����Բ���̵��������ı�����������ֵ��������ֱ�ߵ�б���Ƿ�Ϊ��ֵ���ж���֤�������е��⣬����ʱҪ�������⣬ע����Բ���ʵĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $f��x��=x-\frac{1}{x}$ | B�� | f��x��=ex-1 | C�� | $f��x��=x+\frac{4}{x}$ | D�� | f��x��=tanx |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | b��a��c | C�� | c��b��a | D�� | b��c��a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
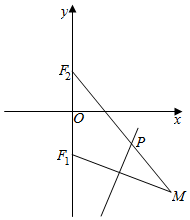 ��ͼ��ʾ����F1��0��-$\sqrt{2}$����F2��0��$\sqrt{2}$��������M����F2�ľ�����4���߶�MF1���д��߽�MF2�ڵ�P������M�仯ʱ����P�Ĺ켣����Ϊ��������
��ͼ��ʾ����F1��0��-$\sqrt{2}$����F2��0��$\sqrt{2}$��������M����F2�ľ�����4���߶�MF1���д��߽�MF2�ڵ�P������M�仯ʱ����P�Ĺ켣����Ϊ��������| A�� | $\frac{x^2}{4}+\frac{y^2}{2}=1$ | B�� | $\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{2}$=1 | C�� | x2+y2=1 | D�� | $\frac{y^2}{4}-\frac{x^2}{2}=1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com