
| A. | a>b>c | B. | b>a>c | C. | c>b>a | D. | b>c>a |
分析 由于$a={log_{\frac{1}{3}}}\frac{1}{2}$=log32<log33=1,b=log23>log22=1,c=log34>log33=1,且b、c都是正数,化简$\frac{b}{c}$>1,从而得到 a、b、c 的大小关系.
解答 解:由于$a={log_{\frac{1}{3}}}\frac{1}{2}$=log32<log33=1,
b=log23>log22=1,
c=log34>log33=1,
$\frac{b}{c}=\frac{lo{g}_{2}3}{lo{g}_{3}4}=\frac{\frac{lg3}{lg2}}{\frac{2lg2}{lg3}}$=$\frac{(lg3)^{2}}{2(lg2)^{2}}>1$,
∴b>c>a.
故选:D.
点评 本题主要考查对数函数的单调性和特殊点,对数的运算性质的应用,比较两个数大小的方法,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
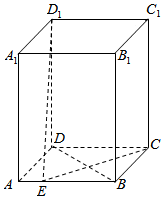 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧棱AA1⊥底面ABCD,已知AB=1,${A}{{A}_1}=\sqrt{3}$,E为AB上一个动点,则D1E+CE的最小值为( )
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧棱AA1⊥底面ABCD,已知AB=1,${A}{{A}_1}=\sqrt{3}$,E为AB上一个动点,则D1E+CE的最小值为( )| A. | $2\sqrt{2}$ | B. | $\sqrt{10}$ | C. | $\sqrt{5}+1$ | D. | $2+\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
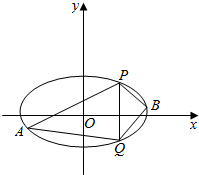 已知椭圆C的中心在原点,离心率等于$\frac{1}{2}$,它的一个短轴端点点恰好是抛物线$y=\frac{{\sqrt{3}}}{24}{x^2}$的焦点.
已知椭圆C的中心在原点,离心率等于$\frac{1}{2}$,它的一个短轴端点点恰好是抛物线$y=\frac{{\sqrt{3}}}{24}{x^2}$的焦点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某市气象部门对该市中心城区近4年春节期间(每年均统计春节假期的前7天)的空气污染指数进行了统计分析,且按是否燃放鞭炮分成两组,得到如图的茎叶图,根据国家最新标准,空气污染指数不超过100的表示没有雾霾,超过100的表示有雾霾.
某市气象部门对该市中心城区近4年春节期间(每年均统计春节假期的前7天)的空气污染指数进行了统计分析,且按是否燃放鞭炮分成两组,得到如图的茎叶图,根据国家最新标准,空气污染指数不超过100的表示没有雾霾,超过100的表示有雾霾.| 燃放 | 未燃放 | 合计 | |
| 有雾霾 | |||
| 无雾霾 | |||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k>5 | B. | 5<k<9 | C. | k<5 | D. | k>9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com