
分析 通过分离常数,借助反比例函数,利用对称中心求出a,b的值.
解答 解:化简函数f(x)=$\frac{2016-bx}{x-a}$=-b+$\frac{-ab+2016}{x-a}$,
因为y=$\frac{1}{x}$的对称中心是(0,0),
所以函数f(x)=-b+$\frac{-ab+2016}{x-a}$的对称中心为(a,-b);
又函数f(x)=$\frac{2016-bx}{x-a}$的对称中心为(1,2),
所以a=1,b=-2;
所以$\overrightarrow{m}$=(1,-2),|$\overrightarrow{m}$|=$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 本题考查了函数的对称中心的求法,反比例函数的对称中心的应用,函数的图象的变换,也考查了分析问题解决问题的能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
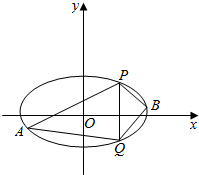 已知椭圆C的中心在原点,离心率等于$\frac{1}{2}$,它的一个短轴端点点恰好是抛物线$y=\frac{{\sqrt{3}}}{24}{x^2}$的焦点.
已知椭圆C的中心在原点,离心率等于$\frac{1}{2}$,它的一个短轴端点点恰好是抛物线$y=\frac{{\sqrt{3}}}{24}{x^2}$的焦点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com