Question

8．设点O在△ABC内部，且有$\overrightarrow{OA}$+2$\overrightarrow{OB}$+3$\overrightarrow{OC}$=$\overrightarrow{0}$，则△BOC、△AOC和△AOB这三个三角形的面积比为1：2：3．

Answer 1

分析 根据向量线性运算的几何意义作出平行四边形，利用相似三角形得出各个小三角形与△ABC的面积比．

解答 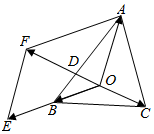解：延长OB至E，使得$\overrightarrow{OE}=2\overrightarrow{OB}$，以OA，OE为邻边作平行四边形OEFA，
则$\overrightarrow{OF}=\overrightarrow{OA}+2\overrightarrow{OB}$，
∵$\overrightarrow{OA}$+2$\overrightarrow{OB}$+3$\overrightarrow{OC}$=$\overrightarrow{0}$，∴$\overrightarrow{OA}+2\overrightarrow{OB}=-3\overrightarrow{OC}$．
∴OF=3OC．
∵△OBD∽△FAD，∴$\frac{OD}{DF}=\frac{OB}{AF}=\frac{1}{2}$，
∴OF=3OD．
∴OD=OC，
∴S_△AOB=$\frac{1}{2}$S_△ABC．
同理可得：S_△BOC=$\frac{1}{6}$S_△ABC．S_△AOC=$\frac{1}{3}$S_△ABC．
∴S_△BOC：S_△AOC：S_△AOB=$\frac{1}{6}：\frac{1}{3}：\frac{1}{2}$=1：2：3．

点评 本题考查了平面向量的线性运算的几何意义，属于中档题．