
分析 分别求出p,q为真时的m的范围,取交集即可.
解答 解:已知p:?x∈[$\frac{1}{4}$,$\frac{1}{2}$],2x<m(x2+1),
故m>$\frac{2x}{{x}^{2}+1}$,
令g(x)=$\frac{2x}{{x}^{2}+1}$,则g(x)在[$\frac{1}{4}$,$\frac{1}{2}$]递增,
故g(x)≤g($\frac{1}{2}$)=$\frac{4}{5}$,
故p为真时:m>$\frac{4}{5}$;
q:函数f(x)=4x+2x+1+m-1=(2x+1)2+m-2,
令f(x)=0,得2x=$\sqrt{2-m}$-1,
若f(x)存在零点,
则$\sqrt{2-m}$-1>0,解得:m<1,
故q为真时,m<1;若“p且q”为真命题,
则实数m的取值范围是:($\frac{4}{5}$,1),
故答案为:($\frac{4}{5}$,1).
点评 本题考查了复合命题的判断,考查函数恒成立问题以及指数函数的性质,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
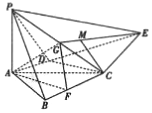 在四棱锥P-ABCE中,PA⊥底面ABCE,CD⊥AE,AC平分∠BAD,G为PC的中点,PA=AD=2,BC=DE,AB=3,CD=2$\sqrt{3}$,F,M分别为BC,EG上一点,且AF∥CD.
在四棱锥P-ABCE中,PA⊥底面ABCE,CD⊥AE,AC平分∠BAD,G为PC的中点,PA=AD=2,BC=DE,AB=3,CD=2$\sqrt{3}$,F,M分别为BC,EG上一点,且AF∥CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -9 | B. | 9 | C. | 6 | D. | -6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an=n | B. | an=n2 | C. | an=$\frac{n}{2}$ | D. | an=$\frac{{n}^{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{2}-1$ | D. | $2-\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
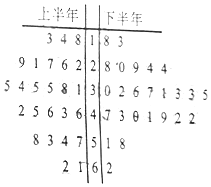 自贡某工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示(如图).已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元
自贡某工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示(如图).已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com