
分析 (Ⅰ)由题意,|x+1|+|x-3|-m≥0恒成立,利用基本不等式,可得求m的取值范围;
(Ⅱ)m的最大值为4,关于x的不等式:|x-3|-2x≤4,分类讨论,即可解关于x的不等式.
解答 解:(Ⅰ)由题意,|x+1|+|x-3|-m≥0恒成立.
∵|x+1|+|x-3|≥|(x+1)-)x-3)|=4,
∴m≤4;
(Ⅱ)m的最大值为4,关于x的不等式:|x-3|-2x≤4.
∴$\left\{\begin{array}{l}{x≥3}\\{x-3-2x≤4}\end{array}\right.$或$\left\{\begin{array}{l}{x<3}\\{3-x-2x≤4}\end{array}\right.$,
∴x≥3或-$\frac{1}{3}$≤x<3,
∴不等式的解集为{x|x≥-$\frac{1}{3}$}.
点评 本题考查恒成立问题,考查绝对值不等式的解法,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{2}$ | B. | 6π | C. | 8π | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,一张A4纸的长、宽分别为2$\sqrt{2}$a,2a,A,B,C,D分别是其四条边的中点,现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,关于该多面体的下列命题,正确的是①②③④.(写出所有正确命题的序号).
如图,一张A4纸的长、宽分别为2$\sqrt{2}$a,2a,A,B,C,D分别是其四条边的中点,现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,关于该多面体的下列命题,正确的是①②③④.(写出所有正确命题的序号).查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
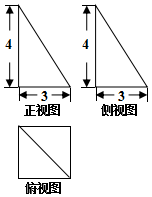
| A. | 10 | B. | $\sqrt{34}$ | C. | 5 | D. | $\frac{{\sqrt{34}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com