已知焦距为2$\sqrt{2}$的椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的右顶点为A.直线y=$\frac{4}{3}$与椭圆C交于P.Q两点.Q在x轴上的射影为B.且四边形ABPQ是平行四边形．(1)求椭圆C的方程,(2)斜率为k的直线l与椭圆C交于两个不同的点M.N．(i)若直线l过原点且与坐� 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

4．已知焦距为2$\sqrt{2}$的椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右顶点为A，直线y=$\frac{4}{3}$与椭圆C交于P、Q两点（P在Q的左边），Q在x轴上的射影为B，且四边形ABPQ是平行四边形．
（1）求椭圆C的方程；
（2）斜率为k的直线l与椭圆C交于两个不同的点M，N．
（i）若直线l过原点且与坐标轴不重合，E是直线3x+3y-2=0上一点，且△EMN是以E为直角顶点的等腰直角三角形，求k的值
（ii）若M是椭圆的左顶点，D是直线MN上一点，且DA⊥AM，点G是x轴上异于点M的点，且以DN为直径的圆恒过直线AN和DG的交点，求证：点G是定点．

分析（1）由题意可得c=$\sqrt{2}$，直线y=$\frac{4}{3}$代入椭圆方程，求得P，Q的横坐标，可得|AB|，由四边形ABPQ是平行四边形，
可得|AB|=|PQ|，解方程可得b，由a，b，c的关系可得a，进而得到椭圆方程；
（2）（i）由直线y=kx代入椭圆方程，求得M的坐标，由△EMN是以E为直角顶点的等腰直角三角形，可设E（m，$\frac{2}{3}$-m），求出E到直线kx-y=0的距离d，由题意可得OE⊥MN，|OM|=d，解方程可得k的值；
（ii）由M（-2，0），可得直线MN的方程为y=k（x+2），代入椭圆方程，可得x的方程，运用韦达定理，可得N的坐标，设G（t，0），（t≠-2），由题意可得D（2，4k），A（2，0），以DN为直径的圆恒过直线AN和DG的交点，可得AN⊥DG，运用两直线垂直的条件，可得斜率之积为-1，解方程可得t=0，即可得到定点．

解答解：（1）由题意可得2c=2$\sqrt{2}$，即c=$\sqrt{2}$，
直线y=$\frac{4}{3}$代入椭圆方程可得$\frac{{x}^{2}}{{a}^{2}}$+$\frac{16}{9{b}^{2}}$=1，
解得x=±a$\sqrt{1-\frac{16}{9{b}^{2}}}$，
可得|AB|=a-a$\sqrt{1-\frac{16}{9{b}^{2}}}$，
由四边形ABPQ是平行四边形，
可得|AB|=|PQ|=2a$\sqrt{1-\frac{16}{9{b}^{2}}}$，
解得b=$\sqrt{2}$，a=$\sqrt{{b}^{2}+{c}^{2}}$=2，
可得椭圆的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1；
（2）（i）由直线y=kx代入椭圆方程，可得（1+2k²）x²=4，
解得x=±$\frac{2}{\sqrt{1+2{k}^{2}}}$，
可设M（$\frac{2}{\sqrt{1+2{k}^{2}}}$，$\frac{2k}{\sqrt{1+2{k}^{2}}}$），
由△EMN是以E为直角顶点的等腰直角三角形，
可设E（m，$\frac{2}{3}$-m），E到直线kx-y=0的距离为d=$\frac{|km+m-\frac{2}{3}|}{\sqrt{1+{k}^{2}}}$，
即有OE⊥MN，|OM|=d，
即为$\frac{\frac{2}{3}-m}{m}$=-$\frac{1}{k}$，$\sqrt{\frac{4+4{k}^{2}}{1+2{k}^{2}}}$=$\frac{|km+m-\frac{2}{3}|}{\sqrt{1+{k}^{2}}}$，
由m=$\frac{2k}{3（k-1）}$，代入第二式，化简整理可得7k²-18k+8=0，
解得k=2或$\frac{4}{7}$；
（ii）证明：由M（-2，0），可得直线MN的方程为y=k（x+2），
代入椭圆方程可得，（1+2k²）x²+8k²x+8k²-4=0，
可得-2+x_N=-$\frac{8{k}^{2}}{1+2{k}^{2}}$，
解得x_N=$\frac{2-4{k}^{2}}{1+2{k}^{2}}$，
y_N=k（x_N+2）=$\frac{4k}{1+2{k}^{2}}$，即N（$\frac{2-4{k}^{2}}{1+2{k}^{2}}$，$\frac{4k}{1+2{k}^{2}}$），
设G（t，0），（t≠-2），由题意可得D（2，4k），A（2，0），
以DN为直径的圆恒过直线AN和DG的交点，
可得AN⊥DG，
即有k_AN•k_DG=-1，
即为$\frac{4k}{2-4{k}^{2}-2-4{k}^{2}}$•$\frac{4k}{2-t}$=-1，
解得t=0．
故点G是定点，即为原点（0，0）．

点评本题考查椭圆方程的求法，注意运用椭圆的性质和平行四边形的性质，考查直线与椭圆的位置关系，注意联立方程组，解方程或运用韦达定理，考查直径所对圆周角为直角，两直线垂直的条件：斜率之积为-1，同时考查点到直线的距离公式，以及化简整理的运算能力，综合性强，属于中档题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

14．设{a_n}是公差不为0的等差数列，a₁=2且a₁，a₃，a₆成等比数列，则{a_n}的前10项和S₁₀=$\frac{85}{2}$．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

15．已知函数f（x）=x²+ax+b（a，b∈R）在区间（0，1）内有两个零点，是3a+b的取值范围是（-5，0）．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

12．设函数f（x）=|x-1|-|2x+1|的最大值为m．
（1）作出函数f（x）的图象；
（2）若a²+2c²+3b²=m，求ab+2bc的最大值．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

19．已知某几何体的三视图如图所示，则该几何体的体积为（　　）

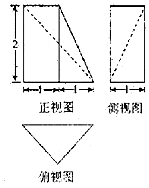
A．

$\frac{2}{3}$

B．

$\frac{4}{3}$

C．

D．

$\frac{8}{3}$

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

9．已知数列{a_n}满足${a_1}=1，|{{a_n}-{a_{n-1}}}|=\frac{1}{2^n}（{n≥2，n∈N}）$，且{a_2n-1}是递减数列，{a_2n}是递增数列，则5-6a₁₀=$\frac{1}{512}$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

16．已知函数f（x）=$\sqrt{|x+1|+|x-3|-m}$的定义域为R．
（Ⅰ）求m的取值范围；
（Ⅱ）若m的最大值为n，解关于x的不等式：|x-3|-2x≤2n-4．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

13．已知圆O的有n条弦，且任意两条弦都彼此相交，任意三条弦不共点，这n条弦将圆O分成了a_n个区域，（例如：如图所示，圆O的一条弦将圆O分成了2（即a₁=2）个区域，圆O的两条弦将圆O分成了4（即a₂=4）个区域，圆O的3条弦将圆O分成了7（即a₃=7）个区域），以此类推，那么a_n+1与a_n（n≥2）之间的递推式关系为：a_n+1=a_n+n+1

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

14．三棱锥P-ABC中，侧棱PA=2，PB=PC=$\sqrt{6}$，则当三棱锥P-ABC的三个侧面的面积和最大时，经过点P，A，B，C的球的表面积是（　　）

A．

4π

B．

8π

C．

12π

D．

16π

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学