
 已知函数f(x)=$\left\{\begin{array}{l}{f_1}(x),x∈[{0,\frac{1}{2}})\\{f_2}(x),x∈[{\frac{1}{2},1}]\end{array}$,其中f1(x)=-2(x-$\frac{1}{2}$)2+1,f2(x)=-2x+2.
已知函数f(x)=$\left\{\begin{array}{l}{f_1}(x),x∈[{0,\frac{1}{2}})\\{f_2}(x),x∈[{\frac{1}{2},1}]\end{array}$,其中f1(x)=-2(x-$\frac{1}{2}$)2+1,f2(x)=-2x+2.分析 (1)根据解析式可得函数的图象;
(2)根据图象写出y=f(x)的单调增区间;
(3)根据分段函数,建立方程关系,解方程即可得到结论.
解答 解:(1)如图所示:
(2)单调增区间$[{0,\frac{1}{2}}]$,
(3)若${x_0}∈[{0,\frac{1}{2}})$,
则${x_1}=f({x_0})=-2{({x_0}-\frac{1}{2})^2}+1$.
此时$\frac{1}{2}≤{x_1}<1$,
∴$f({x_1})=-2{x_1}+2=-2[{-2{{({x_0}-\frac{1}{2})}^2}+1}]+2=4{({x_0}-\frac{1}{2})^2}={x_0}$
整理得4x02-5x0+1=0,
解得x0=1(舍)或${x_0}=\frac{1}{4}$.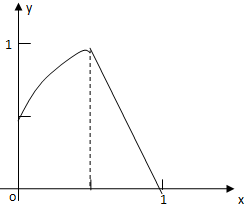
点评 本题主要考查了分段函数的函数解析式的应用,解题的关键是需要根据不同的x确定对应的解析式.


科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {1,3} | C. | {2,5} | D. | {4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | 4 | C. | -4$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{1}{15},\frac{1}{6}}]$ | B. | $({\frac{1}{15},\frac{1}{4}}]$ | C. | $({\frac{1}{6},\frac{1}{4}}]$ | D. | $({\frac{1}{4},\frac{5}{18}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-1,-\frac{1}{2}}]$ | B. | $[{-\frac{1}{2},0})$ | C. | [1,+∞) | D. | $[{-\frac{1}{2},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com