
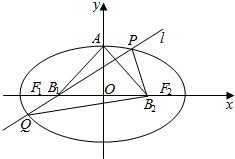
 如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1、F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为1的直角三角形.
如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1、F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为1的直角三角形.分析 (1)由△AB1B2是面积为1的等腰直角三角形知|OA|=|OB1|=1,从而求a,b,c即可;
(2)分类讨论,从而设直线l的方程为y=k(x+1),(k≠0),从而联立方程化简得(5k2+1)x2+10k2x+5k2-5=0,从而利用平面向量化简即可.
解答 解:(1)∵△AB1B2是面积为1的直角三角形,
∴△AB1B2是面积为1的等腰直角三角形,
∴|OA|=|OB1|=1,
∴b=|OA|=1,c=2|OB1|=2,
∴a=$\sqrt{5}$,e=$\frac{2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,
∴标准方程为$\frac{{x}^{2}}{5}$+y2=1.
(2)①当直线l与x轴垂直时,显然PB2与QB2不垂直,
②当直线l与x轴重合时,显然PB2与QB2重合,故不成立,
③设直线l的方程为y=k(x+1),(k≠0),
联立方程得$\left\{\begin{array}{l}{y=k(x+1)}\\{\frac{{x}^{2}}{5}+{y}^{2}=1}\end{array}\right.$,
即(5k2+1)x2+10k2x+5k2-5=0,
设P(x1,y1),Q(x2,y2),
则x1+x2=-$\frac{10{k}^{2}}{5{k}^{2}+1}$,x1x2=$\frac{5{k}^{2}-5}{5{k}^{2}+1}$,
∵PB2⊥QB2,
∴$\overrightarrow{{B}_{2}P}$•$\overrightarrow{{B}_{2}Q}$=0,
∴(x1-1,y1)•(x2-1,y2)=0,
∴(x1-1)(x2-1)+y1y2=0,
∴x1x2-(x1+x2)+1+k2(x1+1)(x2+1)=0,
即(k2+1)x1x2+(k2-1)(x1+x2)+1+k2=0,
即(k2+1)$\frac{5{k}^{2}-5}{5{k}^{2}+1}$-(k2-1)$\frac{10{k}^{2}}{5{k}^{2}+1}$+1+k2=0,
即16k2-4=0,
解得,k=$\frac{1}{2}$或k=-$\frac{1}{2}$;
故直线l的方程为:y=$\frac{1}{2}$(x+1)或y=-$\frac{1}{2}$(x+1),
即l的方程为:x-2y+1=0或x+2y+1=0.
点评 本题考查了数形结合的思想应用及分类讨论的思想应用,同时考查了直线与圆锥曲线的关系应用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
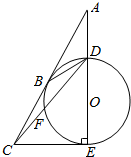 如图,由圆O外一点A引圆的切线AB和割线ADE,B为切点,DE为圆O的直径,且AD=DB.延长AB至C使得CE与圆O相切,连结CD交圆O于点F.
如图,由圆O外一点A引圆的切线AB和割线ADE,B为切点,DE为圆O的直径,且AD=DB.延长AB至C使得CE与圆O相切,连结CD交圆O于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y-3=0 | B. | x+y-3=0或2x+5y=0 | ||
| C. | x-y-7=0或2x+5y=0 | D. | x-y-7=0或x+y-3=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com