
分析 (1)(x+$\frac{1}{2}}$)n的展开式中前3项的系数成等差数列,可得:2${∁}_{n}^{1}×\frac{1}{2}$=1+${∁}_{n}^{2}×(\frac{1}{2})^{2}$,解得n=8,由(x+$\frac{1}{2}}$)n=a0+a1x+a2x2+…+anxn,令x=0,可得:a0.
(2)由二项式系数的单调性可得:${∁}_{8}^{4}$最大.
(3)$(x+\frac{1}{2})^{8}$的展开式的通项公式:Tr+1=${∁}_{8}^{r}{x}^{8-r}×(\frac{1}{2})^{r}$=$(\frac{1}{2})^{r}{∁}_{8}^{r}$x8-r,由$\left\{\begin{array}{l}{(\frac{1}{2})^{r}{∁}_{8}^{r}≥(\frac{1}{2})^{r-1}{∁}_{8}^{r-1}}\\{(\frac{1}{2})^{r}{∁}_{8}^{r}≥(\frac{1}{2})^{r+1}{∁}_{8}^{r+1}}\end{array}\right.$,解得r即可得出.
解答 解:(1)(x+$\frac{1}{2}}$)n的展开式中前3项的系数分别为:1,${∁}_{n}^{1}×\frac{1}{2}$,${∁}_{n}^{2}×(\frac{1}{2})^{2}$,
由于它们成等差数列,∴2${∁}_{n}^{1}×\frac{1}{2}$=1+${∁}_{n}^{2}×(\frac{1}{2})^{2}$,化为n2-9n+8=0,
解得n=8或n=1(舍去),
由(x+$\frac{1}{2}}$)n=a0+a1x+a2x2+…+anxn,
令x=0,可得:a0=$(\frac{1}{2})^{8}$=$\frac{1}{256}$.
(2)由二项式系数的单调性可得:${∁}_{8}^{4}$最大,可得:$C_8^4=70$.
(3)$(x+\frac{1}{2})^{8}$的展开式的通项公式:Tr+1=${∁}_{8}^{r}{x}^{8-r}×(\frac{1}{2})^{r}$=$(\frac{1}{2})^{r}{∁}_{8}^{r}$x8-r,
由$\left\{\begin{array}{l}{(\frac{1}{2})^{r}{∁}_{8}^{r}≥(\frac{1}{2})^{r-1}{∁}_{8}^{r-1}}\\{(\frac{1}{2})^{r}{∁}_{8}^{r}≥(\frac{1}{2})^{r+1}{∁}_{8}^{r+1}}\end{array}\right.$,解得2≤r≤3,
∴r=2或3.
∴系数最大的项是:7x5或7x6.
点评 本题考查了二项式定理的应用、不等式的解法、等差数列的通项公式及其性质,考查了推理能力与计算能力,属于中档题.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
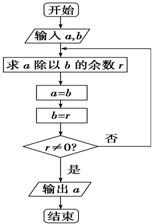 我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大的创举,这个伟大创举与古老的算法--“辗转相除法”实质一样,如图的程序框图源于“辗转相除法”.当输入a=6102,b=2016时,输出的a=18.
我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大的创举,这个伟大创举与古老的算法--“辗转相除法”实质一样,如图的程序框图源于“辗转相除法”.当输入a=6102,b=2016时,输出的a=18.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com