
在平面直角坐标系 中,已知圆
中,已知圆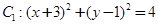 和圆
和圆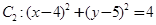 .
.
(1)若直线 过点
过点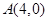 ,且被圆
,且被圆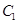 截得的弦长为
截得的弦长为 ,求直线
,求直线 的方程;
的方程;
(2)设 为平面上的点,满足:存在过点
为平面上的点,满足:存在过点 的无穷多对互相垂直的直线
的无穷多对互相垂直的直线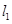 和
和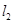 ,它们分别与圆
,它们分别与圆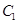 和圆
和圆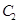 相交,且直线
相交,且直线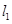 被圆
被圆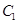 截得的弦长与直线
截得的弦长与直线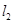 被圆
被圆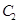 截得的弦长相等,试求所有满足条件的点
截得的弦长相等,试求所有满足条件的点 的坐标.
的坐标.
(1)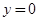 或
或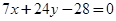 ;(2)
;(2) 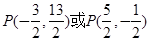 .
.
解析试题分析:(1)涉及到圆的弦长问题,我们一般利用弦心距,弦的一半,相应半径所构成的直角三角形,本题中由弦长为 ,半径为2,可求得弦心距为1,此即为圆心到直线的距离,利用点到直线的距离公式,可求得斜率
,半径为2,可求得弦心距为1,此即为圆心到直线的距离,利用点到直线的距离公式,可求得斜率 .利用方程思想求
.利用方程思想求 时要注意直线斜率不存在即直线与
时要注意直线斜率不存在即直线与 轴垂直的情形.否则可能漏.(2)由(1)的分析可知直线
轴垂直的情形.否则可能漏.(2)由(1)的分析可知直线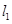 被圆
被圆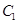 截得的弦长与直线
截得的弦长与直线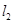 被圆
被圆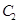 截得的弦长相等可得圆心
截得的弦长相等可得圆心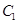 到直线
到直线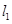 的距离与圆心
的距离与圆心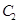 到直线
到直线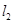 距离相等,所以我们可设
距离相等,所以我们可设 点坐标为
点坐标为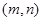 ,直线
,直线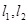 的方程分别为
的方程分别为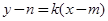 ,
,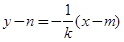 ,利用圆心
,利用圆心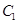 到直线
到直线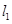 的距离与圆心
的距离与圆心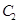 到直线
到直线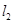 距离相等列出关于
距离相等列出关于 的方程,再转化为关于
的方程,再转化为关于 的方程有无穷解问题,从而得解.
的方程有无穷解问题,从而得解.
试题解析:(1)设直线 的方程为
的方程为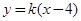 ,即
,即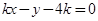
由垂径定理得圆心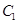 到直线
到直线 的距离
的距离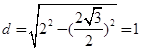
结合点到直线的距离公式得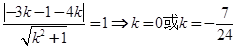
所求直线 的方程为
的方程为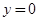 或
或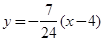 ,即
,即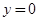 或
或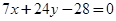
(2)设点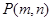 ,直线
,直线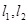 的方程分别为
的方程分别为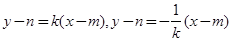
即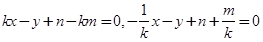
由题意可知圆心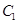 到直线
到直线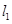 的距离等于
的距离等于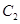 到直线
到直线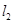 的距离
的距离
即 ,化简得
,化简得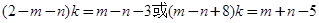 ,关于
,关于 的方程由无穷多解,则有
的方程由无穷多解,则有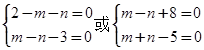 ,故
,故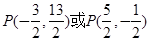 .
.
考点:(1)点到直线距离公式;(2)方程解的个数问题.


科目:高中数学 来源: 题型:解答题
已知椭圆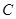 的中心为直角坐标系
的中心为直角坐标系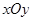 的原点,焦点在
的原点,焦点在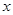 轴上,它的一个顶点到两个焦点的距离分别是7和1.
轴上,它的一个顶点到两个焦点的距离分别是7和1.
(1)求椭圆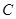 的方程;
的方程;
(2)若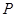 为椭圆
为椭圆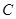 的动点,
的动点,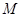 为过
为过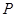 且垂直于
且垂直于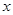 轴的直线上的点,
轴的直线上的点,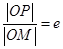 (
(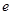 为椭圆的离心率),求点
为椭圆的离心率),求点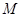 的轨迹方程,并说明轨迹是什么曲线.
的轨迹方程,并说明轨迹是什么曲线.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知A(-5,0),B(5,0),动点P满足|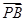 |,
|, |
|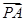 |,8成等差数列.
|,8成等差数列.
(1)求P点的轨迹方程;
(2)对于x轴上的点M,若满足|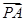 |·|
|·|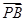 |=
|=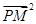 ,则称点M为点P对应的“比例点”.问:对任意一个确定的点P,它总能对应几个“比例点”?
,则称点M为点P对应的“比例点”.问:对任意一个确定的点P,它总能对应几个“比例点”?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知中心在原点的双曲线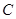 的一个焦点是
的一个焦点是 ,一条渐近线的方程是
,一条渐近线的方程是 。
。
(1)求双曲线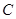 的方程;
的方程;
(2)若以 为斜率的直线
为斜率的直线 与双曲线
与双曲线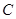 相交于两个不同的点
相交于两个不同的点 ,且线段
,且线段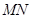 的垂直平分线与两坐标轴围成的三角形的面积为
的垂直平分线与两坐标轴围成的三角形的面积为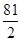 ,求
,求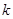 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在 轴上方有一段曲线弧
轴上方有一段曲线弧 ,其端点
,其端点 、
、 在
在 轴上(但不属于
轴上(但不属于 ),对
),对 上任一点
上任一点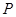 及点
及点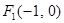 ,
,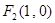 ,满足:
,满足: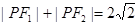 .直线
.直线 ,
,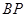 分别交直线
分别交直线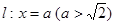 于
于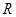 ,
,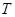 两点.
两点.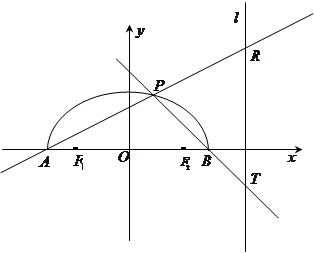
(Ⅰ)求曲线弧 的方程;
的方程;
(Ⅱ)求 的最小值(用
的最小值(用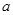 表示);
表示);
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆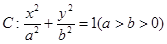 的左右焦点分别是
的左右焦点分别是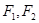 ,离心率
,离心率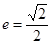 ,
,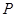 为椭圆上任一点,且
为椭圆上任一点,且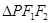 的最大面积为
的最大面积为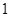 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设斜率为 的直线
的直线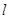 交椭圆
交椭圆 于
于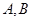 两点,且以
两点,且以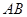 为直径的圆恒过原点
为直径的圆恒过原点 ,若实数
,若实数 满足条件
满足条件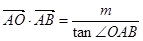 ,求
,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆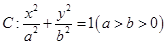 过点
过点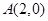 ,离心率为
,离心率为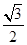 .
.
(Ⅰ)求椭圆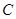 的方程;
的方程;
(Ⅱ)过点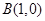 且斜率为
且斜率为 (
(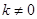 )的直线
)的直线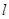 与椭圆
与椭圆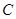 相交于
相交于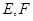 两点,直线
两点,直线 、
、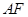 分别交直线
分别交直线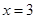 于
于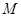 、
、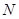 两点,线段
两点,线段 的中点为
的中点为 .记直线
.记直线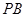 的斜率为
的斜率为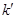 ,求证:
,求证: 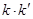 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆的中心在原点,焦点在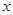 轴上,焦距为
轴上,焦距为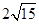 ,且经过点
,且经过点 ,直线
,直线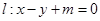 交椭圆于不同的两点A,B.
交椭圆于不同的两点A,B.
(1)求 的取值范围;,
的取值范围;,
(2)若直线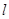 不经过点
不经过点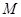 ,求证:直线
,求证:直线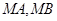 的斜率互为相反数.
的斜率互为相反数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com