
【题目】为了了解某校学生喜欢吃辣是否与性别有关,随机对此校100人进行调查,得到如下的列表:已知在全部100人中随机抽取1人抽到喜欢吃辣的学生的概率为![]() .
.
喜欢吃辣 | 不喜欢吃辣 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 | 100 |
(1)请将上面的列表补充完整;
(2)是否有99.9%以上的把握认为喜欢吃辣与性别有关?说明理由:
下面的临界值表供参考:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: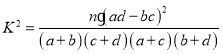 ,其中
,其中![]() )
)
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:高中数学 来源: 题型:
【题目】已知集合A,B,若A不是B的子集,则下列命题中正确的是( )
A.对任意的a∈A,都有aB
B.对任意的b∈B,都有bA
C.存在a0 , 满足a0∈A,a0B
D.存在a0 , 满足a0∈A,a0∈B
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)若函数![]() 在
在![]() 处有极值,求函数
处有极值,求函数![]() 的最大值;
的最大值;
(2)①是否存在实数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立?若存在,求出
上恒成立?若存在,求出![]() 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
②证明:不等式![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,并且
,并且![]() ,数列
,数列![]() 满足:
满足:![]() ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)求数列![]() 的通项公式
的通项公式![]() 及前
及前![]() 项和为
项和为![]() ;
;
(2)求数列![]() 的通项公式
的通项公式![]() 及前
及前![]() 项和为
项和为![]() ;
;
(3)记集合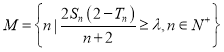 ,若
,若![]() 的子集个数为16,求实数
的子集个数为16,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】围建一个面积为![]() 的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2
的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2![]() 的进出口,如图所示,已知旧墙的维修费用为
的进出口,如图所示,已知旧墙的维修费用为![]() 元/
元/![]() ,新墙的造价为
,新墙的造价为![]() 元/
元/![]() ,设利用的旧墙的长度为
,设利用的旧墙的长度为![]() ,费用为
,费用为![]() 元.
元.
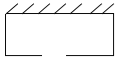
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)试确定![]() 的值,使得修建此矩形场地围墙的总费用最小,并求出最小总费用.
的值,使得修建此矩形场地围墙的总费用最小,并求出最小总费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据统计资料,我国能源生产自1992年以来发展很快,下面是我国能源生产总量(折合亿吨标准煤)的几个统计数据:1992年8.6亿吨,5年后的1997年10.4亿吨,10年后的2002年12.9亿吨.有关专家预测,到2007年我国能源生产总量将达到17.1亿吨,则专家是依据下列哪一类函数作为数学模型进行预测的( )
A.一次函数 B.二次函数 C.指数函数 D.对数函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com