
���� ��1��M���ֱ������Ϊ��0��4�����ɵ�ֱ��l�ķ���Ϊ��$y-4=tan\frac{��}{3}•��x-0��$����y=��sin�ȣ�x=��cos�ȴ��뻯Ϊ������ķ��̣�����C�IJ�������Ϊ$\left\{{\begin{array}{l}{x=cos��}\\{y=sin��}\end{array}}\right.$������cos2��+sin2��=1�ɵ�����C����ͨ���̣�Բ�ĵ�ֱ�ߵľ���d���ɵ�����C��ֱ�ߵľ�������ֵΪd+r��
��2��ֱ��l����б��Ϊ$\frac{��}{3}$����ֱ��l��IJ�������Ϊ$\left\{\begin{array}{l}{x=1+\frac{1}{2}t}\\{y=\frac{\sqrt{3}}{2}t}\end{array}\right.$��tΪ����������${C_1}��\left\{{\begin{array}{l}{x=3cos��}\\{y=2sin��}\end{array}}\right.$������cos2��+sin2��=1�ɵ�����C1����ͨ���̣������������ø���ϵ���Ĺ�ϵ���ɵó���
��� �⣺��1��M���ֱ������Ϊ��0��4������ֱ��l�ķ���Ϊ��$y-4=tan\frac{��}{3}•��x-0��$��$\sqrt{3}x-y+4=0$��
��Ϊ������ķ���Ϊ$\sqrt{3}��cos��-��sin��+4=0$��
����C�IJ�������Ϊ$\left\{{\begin{array}{l}{x=cos��}\\{y=sin��}\end{array}}\right.$����֪����C�ķ���Ϊx2+y2=1��Բ�ĵ�ֱ�ߵľ���$d=\frac{|4|}{{\sqrt{3+1}}}=2$��
������C��ֱ�ߵľ�������ֵΪ2+1=3��
��2��ֱ��l����б��Ϊ$\frac{��}{3}$����ֱ��l��IJ�������Ϊ$\left\{\begin{array}{l}{x=1+\frac{1}{2}t}\\{y=\frac{\sqrt{3}}{2}t}\end{array}\right.$��tΪ��������
��${C_1}��\left\{{\begin{array}{l}{x=3cos��}\\{y=2sin��}\end{array}}\right.$���ɵ�����C1�ķ���Ϊ��$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}=1$��
�����ɵ�$\frac{31}{4}{t}^{2}+4t-32$=0��
��t1t2=-$\frac{128}{31}$��
��|EA||EB|=$\frac{128}{31}$��
���� ���⿼���˼����껯Ϊֱ�����귽�̡�ֱ�ߵIJ������̻�Ϊ��ͨ���̡���Բ�IJ������̣�������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
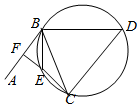 ��ͼ����BCD�ڽ��ڡ�O����B����O������AB����C��Բ�ϣ���ABC�Ľ�ƽ����BE��Բ�ڵ�E����DB��BE����֤��DB=DC��
��ͼ����BCD�ڽ��ڡ�O����B����O������AB����C��Բ�ϣ���ABC�Ľ�ƽ����BE��Բ�ڵ�E����DB��BE����֤��DB=DC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�CD�ǡ�ACB�Ľ�ƽ���ߣ���ACD�����Բ��BC��E�㣮
��ͼ���ڡ�ABC�У�CD�ǡ�ACB�Ľ�ƽ���ߣ���ACD�����Բ��BC��E�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
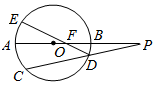 ��ͼ����O��ֱ��AB���ӳ�������CD���ӳ����ཻ�ڵ�P��EΪ��O��һ�㣬$\widehat{AE}$=$\widehat{AC}$��DE��AB�ڵ�F����AB=2BP=8��
��ͼ����O��ֱ��AB���ӳ�������CD���ӳ����ཻ�ڵ�P��EΪ��O��һ�㣬$\widehat{AE}$=$\widehat{AC}$��DE��AB�ڵ�F����AB=2BP=8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ���ɴ˹��ɣ����30��ͼ�αȵ�27��ͼ���еġ���ࣨ������
���ɴ˹��ɣ����30��ͼ�αȵ�27��ͼ���еġ���ࣨ������| A�� | 59�� | B�� | 60�� | C�� | 87�� | D�� | 89�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com