
分析 (1)在△ABC中,由sinA+cosA=$\frac{1}{5}$,平方可由此求得sinA•cosA 的值,由sinA•cosA=-$\frac{12}{25}$,以及sin2A+cos2A=1 可得cosA和sinA 的值,从而求得tanA的值.
(2)由诱导公式化简可求cosα的值,利用诱导公式化简所求后即可得解.
解答 (本题满分为10分)
解:(1)∵sinA+cosA=$\frac{1}{5}$(1),
∴两边平方得1+2sinAcosA=$\frac{1}{25}$,∴sinAcosA=-$\frac{12}{25}$<0,
又0<A<π,可知:sinA>0,cosA<0,
∴sinA-cosA>0,
∵${({sinA-cosA})^2}=1-2sinAcosA=1+\frac{24}{25}=\frac{49}{25}$,
∴$sinA-cosA=\frac{7}{5}.(2)$
由(1),(2)可得$sinA=\frac{4}{5},cosA=-\frac{3}{5}$,
∴$tanA=\frac{sinA}{cosA}=\frac{{\frac{4}{5}}}{{-\frac{3}{5}}}=-\frac{4}{3}$.-----(5分)
(2)∵$cos({α-7π})=cos({7π-α})=-cosα=-\frac{3}{5}$,
∴$cosα=\frac{3}{5}$.
$\begin{array}{l}∴sin(3π+α)•tan({α-\frac{7}{2}π})=sinα•tan({\frac{π}{2}-α})\\=sinα•\frac{{sin({\frac{π}{2}-α})}}{{cos({\frac{π}{2}-α})}}=sinα•\frac{cosα}{sinα}=cosα=\frac{3}{5}.\end{array}$--------------(10分)
点评 本题主要考查同角三角函数的基本关系,诱导公式的应用以及三角函数在各个象限中的符号,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 6个 | B. | 7个 | C. | 8个 | D. | 9个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
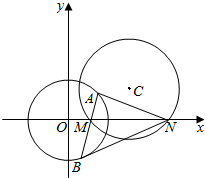 如图,圆C:x2-(1+a)x+y2-ay+a=0.
如图,圆C:x2-(1+a)x+y2-ay+a=0.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
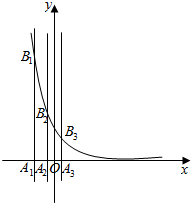 (文)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=($\frac{1}{2}$)x的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.
(文)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=($\frac{1}{2}$)x的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com