
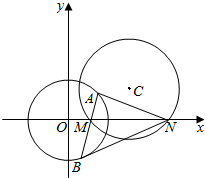
 如图,圆C:x2-(1+a)x+y2-ay+a=0.
如图,圆C:x2-(1+a)x+y2-ay+a=0.分析 (1)由r=$\frac{1}{2}\sqrt{{D}^{2}+{E}^{2}-4F}$,得$\frac{1}{2}\sqrt{(1+a)^{2}+{a}^{2}-4a}$=$\frac{1}{2}$,由此求得a的值,从而求得所求圆C的方程.
(2)先求出所以M(1,0),N(a,0),假设存在实数a,当直线AB与x轴不垂直时,设直线AB的方程为y=k(x-1),代入x2+y2=4,利用韦达定理,根据NA、NB的斜率之和等于零求得a的值.经过检验,当直线AB与x轴垂直时,这个a值仍然满足∠ANM=∠BNM,从而得出结论.
解答 解:(1)由r=$\frac{1}{2}\sqrt{{D}^{2}+{E}^{2}-4F}$
得$\frac{1}{2}\sqrt{(1+a)^{2}+{a}^{2}-4a}$=$\frac{1}{2}$,
所以a=1或a=0,
故所求圆C的方程为x2-2x+y2-y+1=0或x2-x+y2=0;
(2)令y=0,得x2-(1+a)x+a=0,即(x-1)(x-a)=0,求得x=1,或x=a,
所以M(1,0),N(a,0).
假设存在实数a,当直线AB与x轴不垂直时,设直线AB的方程为y=k(x-1),
代入x2+y2=4得,(1+k2)x2-2k2x+k2-4=0,
设A(x1,y1),B(x2,y2),从而x1+x2=$\frac{2{k}^{2}}{1+{k}^{2}}$,x1x2=$\frac{{k}^{2}-4}{1+{k}^{2}}$.
因为NA、NB的斜率之和为$\frac{{y}_{1}}{{x}_{1}-a}$+$\frac{{y}_{2}}{{x}_{2}-a}$=$\frac{k[({x}_{1}-1)({x}_{2}-a)+({x}_{2}-1)({x}_{1}-a)]}{({x}_{1}-a)({x}_{2}-a)}$,
而(x1-1)(x2-a)+(x2-1)(x1-a)=2x1x2-(a+1)(x2+x1)+2a=$\frac{2a-8}{1+{k}^{2}}$,
因为∠ANM=∠BNM,所以,NA、NB的斜率互为相反数,$\frac{{y}_{1}}{{x}_{1}-a}$+$\frac{{y}_{2}}{{x}_{2}-a}$=0,即$\frac{2a-8}{1+{k}^{2}}$=0,得a=4.
当直线AB与x轴垂直时,仍然满足∠ANM=∠BNM,即NA、NB的斜率互为相反数.
综上,存在a=4,使得∠ANM=∠BNM.
点评 本题主要考查求圆的标准方程,直线和圆的位置关系,直线的倾斜角和斜率,属于中档题.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (-∞,1) | C. | (0,1) | D. | (-∞,1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com