
分析 由复合命题的真假判断判断①;求解一元二次不等式,然后结合充分必要条件的判断方法判断②;由椭圆和双曲线的性质判断③;由椭圆和双曲线的定义结合复合命题的真假判断判定④.
解答 解:①p∨q为真命题,包括p、q一真一假,此时p∧q为假命题,故①错误;
②由x2-4x-5>0,得x<-1或x>5,∴“x>5”是“x2-4x-5>0”的充分不必要条件,故②正确;
③曲线$\frac{x^2}{20-m}+\frac{y^2}{6-m}=1\;(m<6)$是焦点在x轴上的椭圆,c2=20-m-6+m=14.
曲线$\frac{x^2}{5-n}+\frac{y^2}{9+n}=1\;(n>5)$是焦点在y轴上的双曲线,∴两曲线焦点不同,故③错误;
④命题p:F1,F2是平面内距离为6的两定点,动点M在此平面内,且满足|MF1|+|MF2|=8,则M点的轨迹是椭圆,此命题为真命题;命题q:F1,F2是平面内距离为6的两定点,动点M在此平面内,且满足||MF1|-|MF2||=6,则M点在轨迹是双曲线,此命题为假命题;则命题p∧?q是真命题,故④正确.
故答案为:②④.
点评 本题考查命题的直接判断与应用,考查了复合命题的真假判断,考查充分必要条件的判断方法,考查圆锥曲线的定义和性质,是基础题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6个 | B. | 7个 | C. | 8个 | D. | 9个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
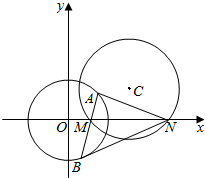 如图,圆C:x2-(1+a)x+y2-ay+a=0.
如图,圆C:x2-(1+a)x+y2-ay+a=0.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com