练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知平面α，β是两个不重合的平面，其法向量分别为n1，n2，给出下列结论：
    ①若n1∥n2，则α∥β；    
    ②若n1∥n2，则α⊥β；
    ③若n1•n2=0，则α⊥β； 
    ④若n1•n2=0，则α∥β．
    其中正确的是（　　）
    A、①③B、①②C、②③D、②④
    考点：命题的真假判断与应用
    专题：空间位置关系与距离,简易逻辑
    分析：直接利用平面的法向量垂直于平面逐一分析四个命题得答案．
    解答： 解：已知平面α，β是两个不重合的平面，其法向量分别为
    n1
    ，
    n2
    ，
    ①若
    n1
    ∥
    n2
    ，则α∥β，命题①正确；    
    ②若
    n1
    ∥
    n2
    ，则α∥β，∴α⊥β不正确，命题②错误；
    ③若
    n1
    •
    n2
    =0    ，则
    n1
    ⊥
    n2
    ，则α⊥β，命题③正确； 
    ④若
    n1
    •
    n2
    =0    ，则
    n1
    ⊥
    n2
    ，∴α∥β不正确，命题④错误．
    ∴正确的命题是①②．
    故选：A．
    点评：本题考查了命题的真假判断与应用，考查了利用平面法向量判断判断两个平面间的位置关系，是基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知f（x）=x2-2|x|，则满足f[f（x）]=-
    1
    2
    的实数x的个数为（　　）
    A、2B、4C、6D、8

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，在Rt△ABC中，AC=1，BC=x，D为斜边AB的中点．将△BCD沿直线CD翻折．若在翻折过程中存在某个位置，使得CB⊥AD，则x的取值范围是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若cos（α-
    π
    6
    ）=
    4
    5
    ，则sin（2α+
    π
    6
    ）的值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f（α）=
    sin(π-α)cos(2π-α)sin(-α+
    3
    2
    π)
    cos(-π-α)cos(-α+
    3
    2
    π)
    ．
    （1）化简f（α）；
    （2）若α是第四象限角，且cos（
    3π
    2
    -α）=
    1
    3
    ，求f（α）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在正三棱锥P-ABC中，三条侧棱两两互相垂直，侧棱长为a，则点P到平面ABC的距离为（　　）
    A、a
    B、
    		2
    2
    a
    C、
    		3
    3
    a
    D、
    		3
    a

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知t为常数，函数y=|x2-4x-t|在区间[0，6]上的最大值为10，则t=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

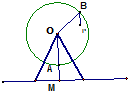    某公园的摩天轮观览车主架示意图如图所示，其中O为轮轴中心，距地面32m（即OM长），巨轮半径为30m，AM=BP=2m，巨轮逆时针旋转且12分钟转动一圈．若点M为P的初始位置（O，A，M共线），经过t分钟，该吊舱P距地面的高度为h（t），则h（t）=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    光线从点A（-3，5）射到x轴上，经反射以后经过点B（2，10），则光线从A到B的距离为（　　）
    A、5
    		2
    B、2
    		5
    C、5
    		10
    D、10
    		5

    查看答案和解析>>

    同步练习册答案