
分析 (1)由题意:定义在R上的奇函数f(x),f(0)=0;x∈(0,2)时,f(x)=$\frac{e^x}{x}$.那么当x∈(-2,0)时,-x∈(0,2),从而可以求解解析式.有最小正周期4,则有f(-2)=f(-2+4)=f(2),得f(2)=0.
可得f(x)在[-2,2]上的解析式;
(2)利于x∈($\frac{1}{2}$,2)解析式,求其导函数;有两个零点,导函数一个解为0,另个大于0或者小于0,即可求实数m的取值范围.
解答 解:由题意:定义在R上的奇函数f(x),f(0)=0;
∵当x∈(0,2)时,f(x)=$\frac{e^x}{x}$,
那么:当x∈(-2,0)时,-x∈(0,2),
则有:f(-x)=$\frac{{e}^{-x}}{-x}$=$\frac{1}{{-xe}^{x}}$=-f(x)
故得:f(x)=$\frac{1}{x{e}^{x}}$
函数有最小正周期4,则有f(-2)=f(-2+4)=f(2),得f(2)=0.
∴f(-2)=f(2)=0
所以:f(x)在[-2,2]上的解析式为:$\left\{\begin{array}{l}{\frac{1}{x{e}^{x}},(-2<x<0)}\\{0,(x=0,x=±2)}\\{\frac{{e}^{x}}{x},(0<x<2)}\end{array}\right.$
(2)∵x∈($\frac{1}{2}$,2)
∴f(x)=$\frac{{e}^{x}}{x}$
那么:函数y=f(x)-2m=$\frac{{e}^{x}}{x}$-2m,(x∈($\frac{1}{2}$,2))
记h(x)=$\frac{{e}^{x}}{x}$-2m,
则有:h′(x)=$\frac{x•{e}^{x}-{e}^{x}}{{x}^{2}}$
令h′(x)=0,解得:x=1
函数y=f(x)-2m在($\frac{1}{2}$,2)内有两个零点:
故得:$\left\{\begin{array}{l}{h(\frac{1}{2})>0}\\{h(1)<0}\\{h(2)>0}\end{array}\right.$或$\left\{\begin{array}{l}{h(\frac{1}{2})<0}\\{h(1)>0}\\{h(2)<0}\end{array}\right.$
解得:$\frac{1}{2}e<m<\frac{1}{4}{e}^{2}$
所以实数m的取值范围为($\frac{1}{2}e$,$\frac{1}{4}{e}^{2}$)
点评 本题考查了分段函数的解析式的求法以及利用导函数的性质求解恒成立问题.属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [3,+∞) | B. | (-∞,-1]∪[3,+∞) | C. | (-∞,1] | D. | R |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
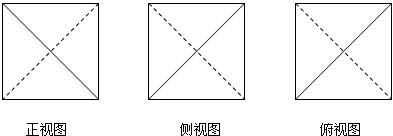
| A. | 3 | B. | 6 | C. | 3+$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com