
分析 (1)求出圆O的方程,运用直线和圆相切的条件,求出b,再由离心率公式和a,b,c的关系,可求出a,进而能求出椭圆方程.
(2)设出A的坐标,代入椭圆方程,求出交点A的坐标,①运用向量的当量积的坐标表示,计算即可得到所求值;②运用三角形面积公式,结合基本不等式即可得到△AOD的面积最大值.
解答 解:(1)由题设知圆O的方程为x2+y2=b2,
∵直线l:x-y+2=0与圆相切,故有$\frac{|2|}{\sqrt{{1}^{2}+(-1)^{2}}}=b$,解得b=$\sqrt{2}$,
∵e=$\frac{c}{a}=\frac{\sqrt{3}}{3}$,∴a2=3c2=3(a2-b2),即a2=3,
∴椭圆C的方程为$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1$.
(2)设A(x0,y0),(x0>0,y0>0),则y0=kx0,
由$\left\{\begin{array}{l}{{y}_{0}=k{x}_{0}}\\{\frac{{{x}_{0}}^{2}}{3}+\frac{{{y}_{0}}^{2}}{2}=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{{x}_{0}=\frac{\sqrt{6}}{\sqrt{2+3{k}^{2}}}}\\{{y}_{0}=\frac{\sqrt{6}k}{\sqrt{2+3{k}^{2}}}}\end{array}\right.$,
①∵$\overrightarrow{OA}•\overrightarrow{OB}$=$\frac{\sqrt{2}×\sqrt{6}}{\sqrt{2+3{k}^{2}}}+\frac{\sqrt{6}k}{\sqrt{2+3{k}^{2}}}$=$\sqrt{6}$,
解得k=$\sqrt{2}$,或k=0(舍),∴k=$\sqrt{2}$.
②∵${S}_{△AOD}=\frac{1}{2}{x}_{0}×2{y}_{0}=k{{x}_{0}}^{2}$
=$\frac{6k}{2+3{k}^{2}}=\frac{6}{\frac{2}{k}+3k}$≤$\frac{6}{2\sqrt{6}}$=$\frac{\sqrt{6}}{2}$.
当且仅当k=$\frac{\sqrt{6}}{3}$时取等号.
∴S△AOD的最大值为$\frac{\sqrt{6}}{2}$.
点评 本题考查椭圆的方程的求法,注意运用离心率公式和直线与圆相切的条件:d=r,同时考查直线方程和圆方程联立,求交点,考查向量的数量积的坐标表示和基本不等式求最值的方法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 必存在平面α使得a∥α,b∥α | |
| B. | 必存在平面α使得a,b与α所成角相等 | |
| C. | 必存在平面α使得a?α,b⊥α | |
| D. | 必存在平面α使得a,b与α的距离相等 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
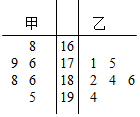 在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图:
在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{5}{4}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{10}$,0)(-$\sqrt{10}$,0) | B. | (0,$\sqrt{10}$),(0,-$\sqrt{10}$) | C. | (0,3)(0,-3) | D. | (3,0),(-3,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com