
【题目】已知函数![]() 的定义域为
的定义域为![]() ,其中
,其中![]() 为常数;
为常数;
(1)若![]() ,且
,且![]() 是奇函数,求
是奇函数,求![]() 的值;
的值;
(2)若![]() ,
, ![]() ,函数
,函数![]() 的最小值是
的最小值是![]() ,求
,求![]() 的最大值;
的最大值;
(3)若![]() ,在
,在![]() 上存在
上存在![]() 个点
个点![]()
![]() ,满足
,满足![]() ,
, ![]() ,
,
![]() ,使得
,使得![]() ,
,
求实数![]() 的取值范围;
的取值范围;
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】试题分析:(1)因为函数为奇函数,根据奇函数定义可得可得![]() 对任意
对任意![]() 恒成立,变形可得
恒成立,变形可得![]() 对任意
对任意![]() 恒成立,可求
恒成立,可求![]() ;(2)将函数
;(2)将函数![]() 的解析式讨论去掉绝对值号,
的解析式讨论去掉绝对值号, 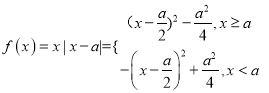 。两段函数的对称轴都为
。两段函数的对称轴都为![]() ,因为
,因为![]() 。讨论
。讨论 ![]() 与-1的大小,可得两段二次函数在区间
与-1的大小,可得两段二次函数在区间![]() 上的单调性,求得最小值。得最小值
上的单调性,求得最小值。得最小值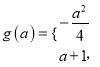 ,求两段的取值范围,取较大的为最大值。(3)由(2)可知
,求两段的取值范围,取较大的为最大值。(3)由(2)可知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,所以
上单调递减,所以![]() ,由绝对值不等式可得
,由绝对值不等式可得![]() ,所以
,所以![]() ,整理得
,整理得![]() ,解得
,解得![]() 为所求.
为所求.
试题解析:解:(1)∵![]() 是奇函数,∴
是奇函数,∴![]() 对任意
对任意![]() 恒成立,
恒成立,
∴![]() ,即
,即![]() 对任意
对任意![]() 恒成立,∴
恒成立,∴![]() ;
;
(2)
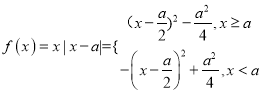 ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
, ![]()
①当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上递减,在
上递减,在![]() 递增,
递增, ![]()
②当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递增,
上单调递增, ![]()
综上所述, 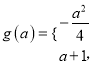 ,
,
若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]()
∴当![]() 时,
时, ![]()
(3)∵![]() ,且
,且![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴![]()
而![]()
要使满足条件的点存在,必须且只需![]() ,即
,即![]() ,解得
,解得![]() 为所求.
为所求.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】第七届世界军人运动会于2019年10月18日至2019年10月27日在中国武汉举行,第七届世界军人运动会是我国第一次承办的综合性国际军事体育赛事,也是继北京奥运会后我国举办的规模最大的国际体育盛会.经过激烈角逐,奖牌榜的前6名依次为中国俄罗斯巴西法国波兰和德国.其中德国队共有45名运动员获得了奖牌,其中金牌10枚银牌15枚铜牌20枚,某大学德语系同学利用分层抽样的方式从德国队获奖选手中抽取9名获奖代表.
(1)请问这9名获奖代表中获金牌银牌铜牌的人数分别为多少人?
(2)从这9人中随机抽取3人,记这3人中银牌选手的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,底面四边形
,底面四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点.
上一点.
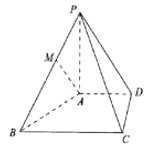
(1)若![]() ,则在线段
,则在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,请确定
?若存在,请确定![]() 点的位置;若不存在,请说明理由
点的位置;若不存在,请说明理由
(2)己知![]() ,若异面直线
,若异面直线![]() 与
与![]() 成
成![]() 角,二而角
角,二而角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,已知曲线![]() ,将曲线
,将曲线![]() 上的点向左平移一个单位,然后纵坐标不变,横坐标轴伸长到原来的2倍,得到曲线
上的点向左平移一个单位,然后纵坐标不变,横坐标轴伸长到原来的2倍,得到曲线![]() ,又已知直线
,又已知直线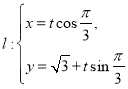 (
(![]() 是参数),且直线
是参数),且直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(I)求曲线![]() 的直角坐标方程,并说明它是什么曲线;
的直角坐标方程,并说明它是什么曲线;
(II)设定点![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com