练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    p：ax2+by2=c为双曲线，q：ab＜0，则p是q的（　　）
    A、充分非必要条件
    B、必要非充分条件
    C、既不充分也不必要条件
    D、充要条件
    考点：必要条件、充分条件与充要条件的判断
    专题：简易逻辑
    分析：p：ax2+by2=c为双曲线，化为
    x2
    c
    a
    +
    y2
    c
    b
    =1    ，可得
    c
    a
    •
    c
    b
    ＜0，于是ab＜0，c≠0．即可判断出．
    解答： 解：p：ax2+by2=c为双曲线，化为
    x2
    c
    a
    +
    y2
    c
    b
    =1    ，则
    c
    a
    •
    c
    b
    ＜0，∴ab＜0，c≠0．
    因此p是q的既不必要不充分条件．
    故选：C．
    点评：本题考查了双曲线的标准方程、充分必要的判定，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    ∫
    0
    -π
    （cosx+ex）dx=（　　）
    A、1-e-π
    B、1+e-π
    C、-e-π
    D、πe-π-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知正三棱柱ABC-A′B′C′（底面为正三角形，侧棱垂直于底面）的正视图和侧视图如图所示．设△ABC、△A′B′C′的中心为O，O′，现将此三棱柱绕直线OO′旋转．射线OA旋转所成的角为x弧度（x可取任一实数，逆时针为正角，顺时针为负角）．对应的俯视图的面积为S（x），则S（x）的最小正周期和值域分别为（　　）
    A、
    2π
    3
    ，[4，8]
    B、
    2π
    3
    ，[4
    		3
    ，8]
    C、
    π
    3
    ，[4，8]
    D、
    π
    3
    ，[4
    		3
    ，8]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知集合A={1，-2，-3，4}，B={x|x=|n|，n∈A}，则A∩B=（　　）
    A、{1，-2}
    B、{-2，-3}
    C、{2，3}
    D、{1，4}

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （文科）双曲线x2-y2=1的焦点坐标为（　　）
    A、（±1，0）
    B、（0，±1）
    C、（±
    		2
    ，0）
    D、（0，±
    		2
    ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知x，y∈R，若p：x＜1且y＜1，q：x+y≥2．则p是￢q的（　　）
    A、充分而不必要条件
    B、必要而不充分条件
    C、充要条件
    D、既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知sin
    θ
    2
    +cos
    θ
    2
    =
    1
    2
    ，则cos2θ=（　　）
    A、-
    3
    4
    B、
    1
    8
    C、-
    1
    8
    D、
    		7
    4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在如图所示的程序框图中输入n=3，结果会输出（　　）
    A、2B、4C、6D、8

    查看答案和解析>>

    科目：高中数学 来源： 题型：

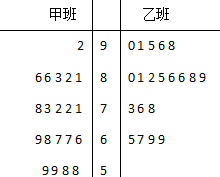    我市某校某数学老师这学期分别用m，n两种不同的教学方式试验高一甲、乙两个班（人数均为60人，入学数学平均分和优秀率都相同，勤奋程度和自觉性都一样）．现随机抽取甲、乙两班各20名的数学期末考试成绩，并作出茎叶图如图所示．
    （Ⅰ）依茎叶图判断哪个班的平均分高？
    （Ⅱ）现从甲班所抽数学成绩不低于80分的同学中随机抽取两名同学，用ξ表示抽到成绩为86分的人数，求ξ的分布列和数学期望；
    （Ⅲ）学校规定：成绩不低于85分的为优秀，作出分类变量成绩与教学方式的2×2列联表，并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关？”
    下面临界值表仅供参考：
    P（K2≥k）0.150.100.050.0250.0100.0050.001
    k2.0722.7063.8415.0246.6357.87910.828
    （参考公式：K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)
    ，其中n=a+b+c+d）

    查看答案和解析>>

    同步练习册答案