
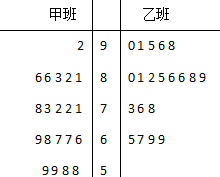
 ����ijУij��ѧ��ʦ��ѧ�ڷֱ���m��n���ֲ�ͬ�Ľ�ѧ��ʽ�����һ�ס��������ࣨ������Ϊ60�ˣ���ѧ��ѧƽ���ֺ������ʶ���ͬ���ڷ̶ܳȺ��Ծ��Զ�һ�������������ȡ�ס��������20������ѧ��ĩ���Գɼ�����������Ҷͼ��ͼ��ʾ��
����ijУij��ѧ��ʦ��ѧ�ڷֱ���m��n���ֲ�ͬ�Ľ�ѧ��ʽ�����һ�ס��������ࣨ������Ϊ60�ˣ���ѧ��ѧƽ���ֺ������ʶ���ͬ���ڷ̶ܳȺ��Ծ��Զ�һ�������������ȡ�ס��������20������ѧ��ĩ���Գɼ�����������Ҷͼ��ͼ��ʾ��| P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| ||
|
| 6 |
| 15 |
| ||||
|
| 8 |
| 15 |
| ||
|
| 1 |
| 15 |
| �� | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 6 |
| 15 |
| 8 |
| 15 |
| 1 |
| 15 |
| 2 |
| 3 |
| �װ� | �Ұ� | �ϼ� | |
| ���� | 3 | 10 | 13 |
| ������ | 17 | 10 | 27 |
| �ϼ� | 20 | 20 | 40 |
| 40��(3��10-10��17)2 |
| 13��27��20��20 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| A����ַDZ�Ҫ���� |
| B����Ҫ�dz������ |
| C���Ȳ����Ҳ����Ҫ���� |
| D����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| a |
| b |
| 3�� |
| 8 |
| �� |
| 4 |
| a |
| b |
| 1 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ij��˾Ϊһ�������豸���������һ�ֳ����α��壬���ܳ�Ϊ4�ף����ֱ���������Խ����۵���ʹ�ã���ͼ��ʾ��ABCD��AB��AD��Ϊ�����α��壬��AC�۵���AB�ۺ�ΪAB�䣬AB�佻DC�ڵ�P�����������ACB��PD��������ʱ����Ч����ã�
ij��˾Ϊһ�������豸���������һ�ֳ����α��壬���ܳ�Ϊ4�ף����ֱ���������Խ����۵���ʹ�ã���ͼ��ʾ��ABCD��AB��AD��Ϊ�����α��壬��AC�۵���AB�ۺ�ΪAB�䣬AB�佻DC�ڵ�P�����������ACB��PD��������ʱ����Ч����ã��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
| 2 |
| BD |
| DA |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 2 |
| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 2 |
| 1 |
| 16 |
| 1 |
| 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| e1 |
| e2 |
| AB |
| e1 |
| e2 |
| BE |
| e1 |
| e2 |
| EC |
| e1 |
| e2 |
| e1 |
| e2 |
| BC |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com